This is the multi-page printable view of this section. Click here to print.
Time series analysis
- 1: Example use cases
- 1.1: Analyze time series data
- 1.2: Anomaly diagnosis for root cause analysis
- 1.3: Time series anomaly detection & forecasting
- 2: series_product()
- 3: make-series operator
- 4: series_abs()
- 5: series_acos()
- 6: series_add()
- 7: series_atan()
- 8: series_cos()
- 9: series_cosine_similarity()
- 10: series_decompose_anomalies()
- 11: series_decompose_forecast()
- 12: series_decompose()
- 13: series_divide()
- 14: series_dot_product()
- 15: series_equals()
- 16: series_exp()
- 17: series_fft()
- 18: series_fill_backward()
- 19: series_fill_const()
- 20: series_fill_forward()
- 21: series_fill_linear()
- 22: series_fir()
- 23: series_fit_2lines_dynamic()
- 24: series_fit_2lines()
- 25: series_fit_line_dynamic()
- 26: series_fit_line()
- 27: series_fit_poly()
- 28: series_floor()
- 29: series_greater_equals()
- 30: series_greater()
- 31: series_ifft()
- 32: series_iir()
- 33: series_less_equals()
- 34: series_less()
- 35: series_log()
- 36: series_magnitude()
- 37: series_multiply()
- 38: series_not_equals()
- 39: series_outliers()
- 40: series_pearson_correlation()
- 41: series_periods_detect()
- 42: series_periods_validate()
- 43: series_seasonal()
- 44: series_sign()
- 45: series_sin()
- 46: series_stats_dynamic()
- 47: series_stats()
- 48: series_subtract()
- 49: series_sum()
- 50: series_tan()
- 51: series_asin()
- 52: series_ceiling()
- 53: series_pow()
1 - Example use cases
1.1 - Analyze time series data
Cloud services and IoT devices generate telemetry you can use to gain insights into service health, production processes, and usage trends. Time series analysis helps you identify deviations from typical baseline patterns.
Kusto Query Language (KQL) has native support for creating, manipulating, and analyzing multiple time series. This article shows how to use KQL to create and analyze thousands of time series in seconds to enable near real-time monitoring solutions and workflows.
Time series creation
Create a large set of regular time series using the make-series operator and fill in missing values as needed.
Partition and transform the telemetry table into a set of time series. The table usually contains a timestamp column, contextual dimensions, and optional metrics. The dimensions are used to partition the data. The goal is to create thousands of time series per partition at regular time intervals.
The input table demo_make_series1 contains 600K records of arbitrary web service traffic. Use the following command to sample 10 records:
demo_make_series1 | take 10
The resulting table contains a timestamp column, three contextual dimension columns, and no metrics:
| TimeStamp | BrowserVer | OsVer | Country/Region |
|---|---|---|---|
| 2016-08-25 09:12:35.4020000 | Chrome 51.0 | Windows 7 | United Kingdom |
| 2016-08-25 09:12:41.1120000 | Chrome 52.0 | Windows 10 | |
| 2016-08-25 09:12:46.2300000 | Chrome 52.0 | Windows 7 | United Kingdom |
| 2016-08-25 09:12:46.5100000 | Chrome 52.0 | Windows 10 | United Kingdom |
| 2016-08-25 09:12:46.5570000 | Chrome 52.0 | Windows 10 | Republic of Lithuania |
| 2016-08-25 09:12:47.0470000 | Chrome 52.0 | Windows 8.1 | India |
| 2016-08-25 09:12:51.3600000 | Chrome 52.0 | Windows 10 | United Kingdom |
| 2016-08-25 09:12:51.6930000 | Chrome 52.0 | Windows 7 | Netherlands |
| 2016-08-25 09:12:56.4240000 | Chrome 52.0 | Windows 10 | United Kingdom |
| 2016-08-25 09:13:08.7230000 | Chrome 52.0 | Windows 10 | India |
Because there are no metrics, build time series representing the traffic count, partitioned by OS:
let min_t = toscalar(demo_make_series1 | summarize min(TimeStamp));
let max_t = toscalar(demo_make_series1 | summarize max(TimeStamp));
demo_make_series1
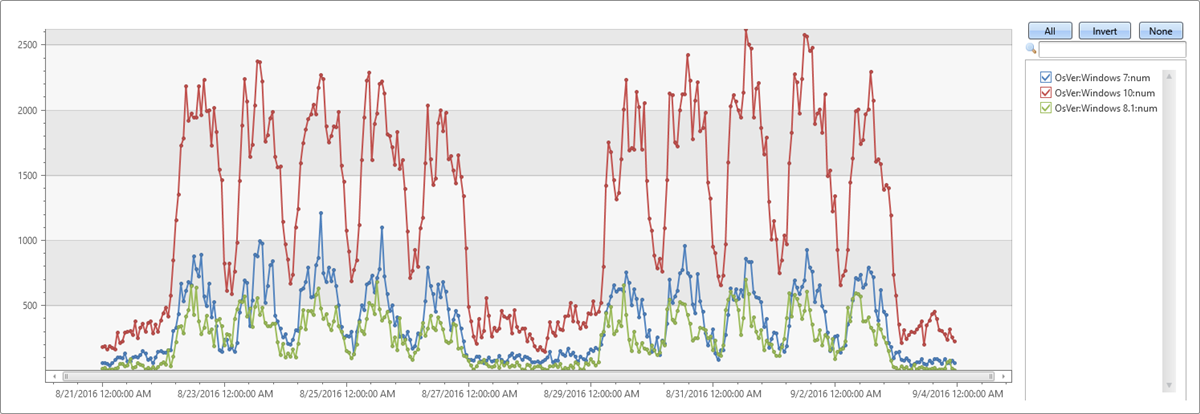
| make-series num=count() default=0 on TimeStamp from min_t to max_t step 1h by OsVer
| render timechart
- Use the
make-seriesoperator to create three time series, where:num=count(): traffic count.from min_t to max_t step 1h: creates the time series in one hour bins from the table’s oldest to newest timestamp.default=0: specifies the fill method for missing bins to create regular time series. Alternatively, useseries_fill_const(),series_fill_forward(),series_fill_backward(), andseries_fill_linear()for different fill behavior.by OsVer: partitions by OS.
- The time series data structure is a numeric array of aggregated values for each time bin. Use
render timechartfor visualization.
The table above has three partitions (Windows 10, Windows 7, and Windows 8.1). The chart shows a separate time series for each OS version:
Time series analysis functions
In this section, we’ll perform typical series processing functions. Once a set of time series is created, KQL supports a growing list of functions to process and analyze them. We’ll describe a few representative functions for processing and analyzing time series.
Filtering
Filtering is a common practice in signal processing and useful for time series processing tasks (for example, smooth a noisy signal, change detection).
- There are two generic filtering functions:
series_fir(): Applying FIR filter. Used for simple calculation of moving average and differentiation of the time series for change detection.series_iir(): Applying IIR filter. Used for exponential smoothing and cumulative sum.
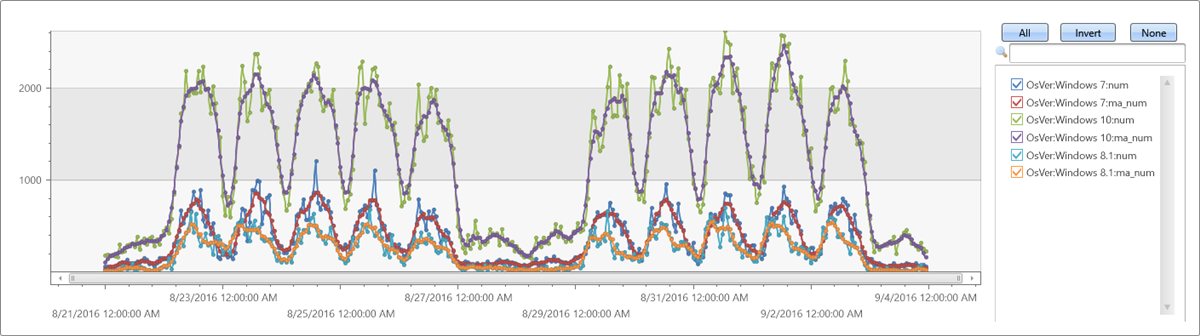
Extendthe time series set by adding a new moving average series of size 5 bins (named ma_num) to the query:
let min_t = toscalar(demo_make_series1 | summarize min(TimeStamp));
let max_t = toscalar(demo_make_series1 | summarize max(TimeStamp));
demo_make_series1
| make-series num=count() default=0 on TimeStamp from min_t to max_t step 1h by OsVer
| extend ma_num=series_fir(num, repeat(1, 5), true, true)
| render timechart
Regression analysis
A segmented linear regression analysis can be used to estimate the trend of the time series.
- Use series_fit_line() to fit the best line to a time series for general trend detection.
- Use series_fit_2lines() to detect trend changes, relative to the baseline, that are useful in monitoring scenarios.
Example of series_fit_line() and series_fit_2lines() functions in a time series query:
demo_series2
| extend series_fit_2lines(y), series_fit_line(y)
| render linechart with(xcolumn=x)
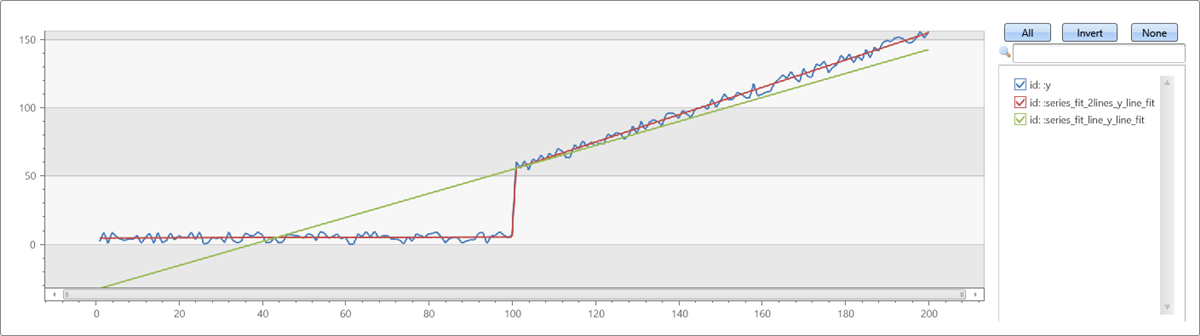
- Blue: original time series
- Green: fitted line
- Red: two fitted lines
Seasonality detection
Many metrics follow seasonal (periodic) patterns. User traffic of cloud services usually contains daily and weekly patterns that are highest around the middle of the business day and lowest at night and over the weekend. IoT sensors measure in periodic intervals. Physical measurements such as temperature, pressure, or humidity may also show seasonal behavior.
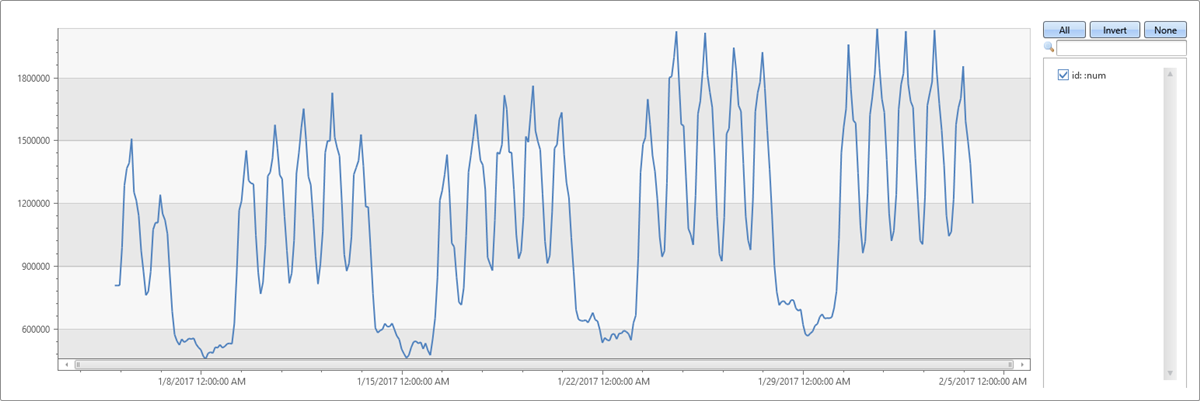
The following example applies seasonality detection on one month traffic of a web service (2-hour bins):
demo_series3
| render timechart
- Use series_periods_detect() to automatically detect the periods in the time series, where:
num: the time series to analyze0.: the minimum period length in days (0 means no minimum)14d/2h: the maximum period length in days, which is 14 days divided into 2-hour bins2: the number of periods to detect
- Use series_periods_validate() if we know that a metric should have specific distinct periods and we want to verify that they exist.
demo_series3
| project (periods, scores) = series_periods_detect(num, 0., 14d/2h, 2) //to detect the periods in the time series
| mv-expand periods, scores
| extend days=2h*todouble(periods)/1d
| periods | scores | days |
|---|---|---|
| 84 | 0.820622786055595 | 7 |
| 12 | 0.764601405803502 | 1 |
The function detects daily and weekly seasonality. The daily scores less than the weekly because weekend days are different from weekdays.
Element-wise functions
Arithmetic and logical operations can be done on a time series. Using series_subtract() we can calculate a residual time series, that is, the difference between original raw metric and a smoothed one, and look for anomalies in the residual signal:
let min_t = toscalar(demo_make_series1 | summarize min(TimeStamp));
let max_t = toscalar(demo_make_series1 | summarize max(TimeStamp));
demo_make_series1
| make-series num=count() default=0 on TimeStamp from min_t to max_t step 1h by OsVer
| extend ma_num=series_fir(num, repeat(1, 5), true, true)
| extend residual_num=series_subtract(num, ma_num) //to calculate residual time series
| where OsVer == "Windows 10" // filter on Win 10 to visualize a cleaner chart
| render timechart
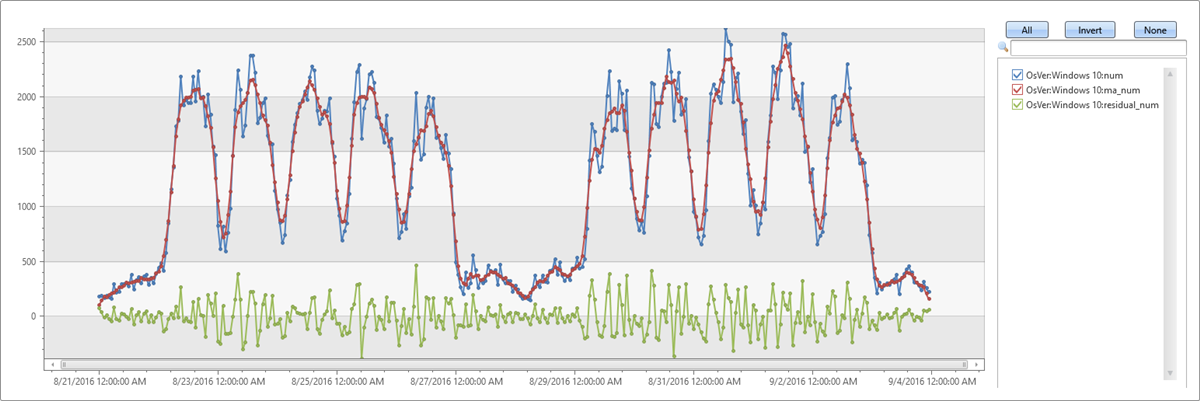
- Blue: original time series
- Red: smoothed time series
- Green: residual time series
Time series workflow at scale
This example shows anomaly detection running at scale on thousands of time series in seconds. To see sample telemetry records for a DB service read count metric over four days, run the following query:
demo_many_series1
| take 4
| TIMESTAMP | Loc | Op | DB | DataRead |
|---|---|---|---|---|
| 2016-09-11 21:00:00.0000000 | Loc 9 | 5117853934049630089 | 262 | 0 |
| 2016-09-11 21:00:00.0000000 | Loc 9 | 5117853934049630089 | 241 | 0 |
| 2016-09-11 21:00:00.0000000 | Loc 9 | -865998331941149874 | 262 | 279862 |
| 2016-09-11 21:00:00.0000000 | Loc 9 | 371921734563783410 | 255 | 0 |
View simple statistics:
demo_many_series1
| summarize num=count(), min_t=min(TIMESTAMP), max_t=max(TIMESTAMP)
| num | min_t | max_t |
|---|---|---|
| 2177472 | 2016-09-08 00:00:00.0000000 | 2016-09-11 23:00:00.0000000 |
A time series in 1-hour bins of the read metric (four days × 24 hours = 96 points) shows normal hourly fluctuation:
let min_t = toscalar(demo_many_series1 | summarize min(TIMESTAMP));
let max_t = toscalar(demo_many_series1 | summarize max(TIMESTAMP));
demo_many_series1
| make-series reads=avg(DataRead) on TIMESTAMP from min_t to max_t step 1h
| render timechart with(ymin=0)
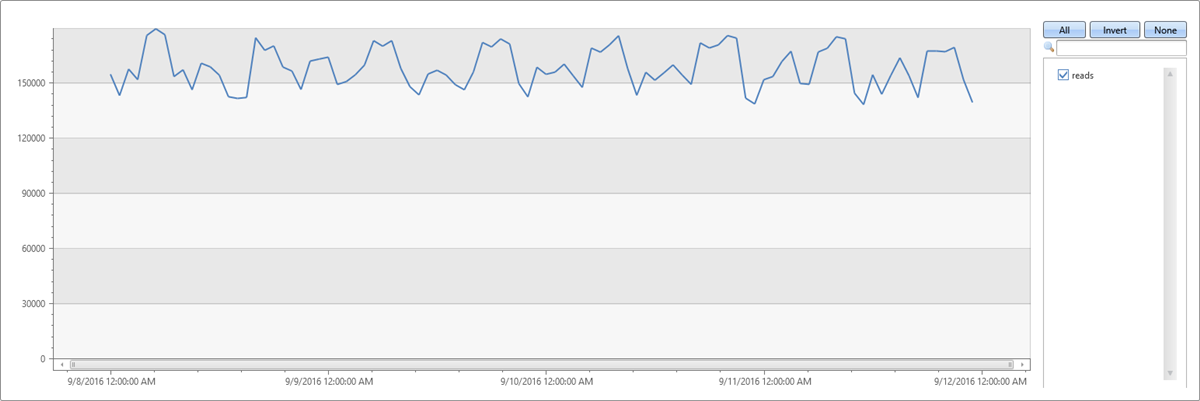
This behavior is misleading because the single normal time series is aggregated from thousands of instances that can have abnormal patterns. Create a time series per instance defined by Loc (location), Op (operation), and DB (specific machine).
How many time series can you create?
demo_many_series1
| summarize by Loc, Op, DB
| count
| Count |
|---|
| 18339 |
Create 18,339 time series for the read count metric. Add the by clause to the make-series statement, apply linear regression, and select the top two time series with the most significant decreasing trend:
let min_t = toscalar(demo_many_series1 | summarize min(TIMESTAMP));
let max_t = toscalar(demo_many_series1 | summarize max(TIMESTAMP));
demo_many_series1
| make-series reads=avg(DataRead) on TIMESTAMP from min_t to max_t step 1h by Loc, Op, DB
| extend (rsquare, slope) = series_fit_line(reads)
| top 2 by slope asc
| render timechart with(title='Service Traffic Outage for 2 instances (out of 18339)')
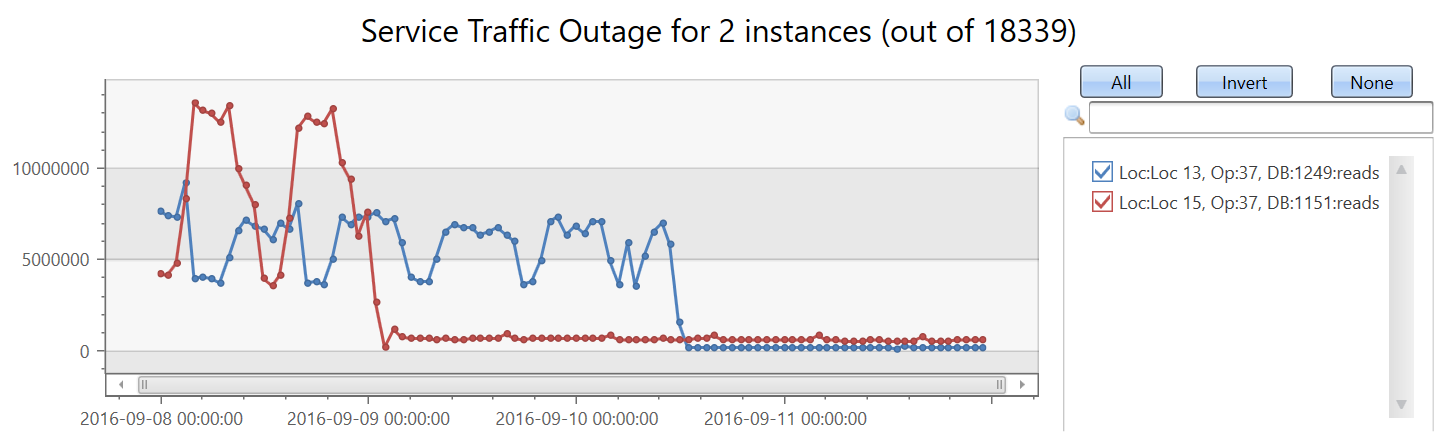
Display the instances:
let min_t = toscalar(demo_many_series1 | summarize min(TIMESTAMP));
let max_t = toscalar(demo_many_series1 | summarize max(TIMESTAMP));
demo_many_series1
| make-series reads=avg(DataRead) on TIMESTAMP from min_t to max_t step 1h by Loc, Op, DB
| extend (rsquare, slope) = series_fit_line(reads)
| top 2 by slope asc
| project Loc, Op, DB, slope
| Loc | Op | DB | slope |
|---|---|---|---|
| Loc 15 | 37 | 1151 | -104,498.46510358342 |
| Loc 13 | 37 | 1249 | -86,614.02919932814 |
In under two minutes, the query analyzes nearly 20,000 time series and detects two with a sudden read count drop.
These capabilities and the platform performance provide a powerful solution for time series analysis.
Related content
- Anomaly detection and forecasting with KQL.
- Machine learning capabilities with KQL.
1.2 - Anomaly diagnosis for root cause analysis
Kusto Query Language (KQL) has built-in anomaly detection and forecasting functions to check for anomalous behavior. Once such a pattern is detected, a Root Cause Analysis (RCA) can be run to mitigate or resolve the anomaly.
The diagnosis process is complex and lengthy, and done by domain experts. The process includes:
- Fetching and joining more data from different sources for the same time frame
- Looking for changes in the distribution of values on multiple dimensions
- Charting more variables
- Other techniques based on domain knowledge and intuition
Since these diagnosis scenarios are common, machine learning plugins are available to make the diagnosis phase easier, and shorten the duration of the RCA.
All three of the following Machine Learning plugins implement clustering algorithms: autocluster, basket, and diffpatterns. The autocluster and basket plugins cluster a single record set, and the diffpatterns plugin clusters the differences between two record sets.
Clustering a single record set
A common scenario includes a dataset selected by a specific criteria such as:
- Time window that shows anomalous behavior
- High temperature device readings
- Long duration commands
- Top spending users
You want a fast and easy way to find common patterns (segments) in the data. Patterns are a subset of the dataset whose records share the same values over multiple dimensions (categorical columns).
The following query builds and shows a time series of service exceptions over the period of a week, in ten-minute bins:
let min_t = toscalar(demo_clustering1 | summarize min(PreciseTimeStamp));
let max_t = toscalar(demo_clustering1 | summarize max(PreciseTimeStamp));
demo_clustering1
| make-series num=count() on PreciseTimeStamp from min_t to max_t step 10m
| render timechart with(title="Service exceptions over a week, 10 minutes resolution")

The service exception count correlates with the overall service traffic. You can clearly see the daily pattern for business days, Monday to Friday. There’s a rise in service exception counts at mid-day, and drops in counts during the night. Flat low counts are visible over the weekend. Exception spikes can be detected using time series anomaly detection.
The second spike in the data occurs on Tuesday afternoon. The following query is used to further diagnose and verify whether it’s a sharp spike. The query redraws the chart around the spike in a higher resolution of eight hours in one-minute bins. You can then study its borders.
let min_t=datetime(2016-08-23 11:00);
demo_clustering1
| make-series num=count() on PreciseTimeStamp from min_t to min_t+8h step 1m
| render timechart with(title="Zoom on the 2nd spike, 1 minute resolution")

You see a narrow two-minute spike from 15:00 to 15:02. In the following query, count the exceptions in this two-minute window:
let min_peak_t=datetime(2016-08-23 15:00);
let max_peak_t=datetime(2016-08-23 15:02);
demo_clustering1
| where PreciseTimeStamp between(min_peak_t..max_peak_t)
| count
| Count |
|---|
| 972 |
In the following query, sample 20 exceptions out of 972:
let min_peak_t=datetime(2016-08-23 15:00);
let max_peak_t=datetime(2016-08-23 15:02);
demo_clustering1
| where PreciseTimeStamp between(min_peak_t..max_peak_t)
| take 20
| PreciseTimeStamp | Region | ScaleUnit | DeploymentId | Tracepoint | ServiceHost |
|---|---|---|---|---|---|
| 2016-08-23 15:00:08.7302460 | scus | su5 | 9dbd1b161d5b4779a73cf19a7836ebd6 | 100005 | 00000000-0000-0000-0000-000000000000 |
| 2016-08-23 15:00:09.9496584 | scus | su5 | 9dbd1b161d5b4779a73cf19a7836ebd6 | 10007006 | 8d257da1-7a1c-44f5-9acd-f9e02ff507fd |
| 2016-08-23 15:00:10.5911748 | scus | su5 | 9dbd1b161d5b4779a73cf19a7836ebd6 | 100005 | 00000000-0000-0000-0000-000000000000 |
| 2016-08-23 15:00:12.2957912 | scus | su5 | 9dbd1b161d5b4779a73cf19a7836ebd6 | 10007007 | f855fcef-ebfe-405d-aaf8-9c5e2e43d862 |
| 2016-08-23 15:00:18.5955357 | scus | su5 | 9dbd1b161d5b4779a73cf19a7836ebd6 | 10007006 | 9d390e07-417d-42eb-bebd-793965189a28 |
| 2016-08-23 15:00:20.7444854 | scus | su5 | 9dbd1b161d5b4779a73cf19a7836ebd6 | 10007006 | 6e54c1c8-42d3-4e4e-8b79-9bb076ca71f1 |
| 2016-08-23 15:00:23.8694999 | eus2 | su2 | 89e2f62a73bb4efd8f545aeae40d7e51 | 36109 | 19422243-19b9-4d85-9ca6-bc961861d287 |
| 2016-08-23 15:00:26.4271786 | ncus | su1 | e24ef436e02b4823ac5d5b1465a9401e | 36109 | 3271bae4-1c5b-4f73-98ef-cc117e9be914 |
| 2016-08-23 15:00:27.8958124 | scus | su3 | 90d3d2fc7ecc430c9621ece335651a01 | 904498 | 8cf38575-fca9-48ca-bd7c-21196f6d6765 |
| 2016-08-23 15:00:32.9884969 | scus | su3 | 90d3d2fc7ecc430c9621ece335651a01 | 10007007 | d5c7c825-9d46-4ab7-a0c1-8e2ac1d83ddb |
| 2016-08-23 15:00:34.5061623 | scus | su5 | 9dbd1b161d5b4779a73cf19a7836ebd6 | 1002110 | 55a71811-5ec4-497a-a058-140fb0d611ad |
| 2016-08-23 15:00:37.4490273 | scus | su3 | 90d3d2fc7ecc430c9621ece335651a01 | 10007006 | f2ee8254-173c-477d-a1de-4902150ea50d |
| 2016-08-23 15:00:41.2431223 | scus | su3 | 90d3d2fc7ecc430c9621ece335651a01 | 103200 | 8cf38575-fca9-48ca-bd7c-21196f6d6765 |
| 2016-08-23 15:00:47.2983975 | ncus | su1 | e24ef436e02b4823ac5d5b1465a9401e | 423690590 | 00000000-0000-0000-0000-000000000000 |
| 2016-08-23 15:00:50.5932834 | scus | su5 | 9dbd1b161d5b4779a73cf19a7836ebd6 | 10007006 | 2a41b552-aa19-4987-8cdd-410a3af016ac |
| 2016-08-23 15:00:50.8259021 | scus | su5 | 9dbd1b161d5b4779a73cf19a7836ebd6 | 1002110 | 0d56b8e3-470d-4213-91da-97405f8d005e |
| 2016-08-23 15:00:53.2490731 | scus | su5 | 9dbd1b161d5b4779a73cf19a7836ebd6 | 36109 | 55a71811-5ec4-497a-a058-140fb0d611ad |
| 2016-08-23 15:00:57.0000946 | eus2 | su2 | 89e2f62a73bb4efd8f545aeae40d7e51 | 64038 | cb55739e-4afe-46a3-970f-1b49d8ee7564 |
| 2016-08-23 15:00:58.2222707 | scus | su5 | 9dbd1b161d5b4779a73cf19a7836ebd6 | 10007007 | 8215dcf6-2de0-42bd-9c90-181c70486c9c |
| 2016-08-23 15:00:59.9382620 | scus | su3 | 90d3d2fc7ecc430c9621ece335651a01 | 10007006 | 451e3c4c-0808-4566-a64d-84d85cf30978 |
Even though there are less than a thousand exceptions, it’s still hard to find common segments, since there are multiple values in each column. You can use the autocluster() plugin to instantly extract a short list of common segments and find the interesting clusters within the spike’s two minutes, as seen in the following query:
let min_peak_t=datetime(2016-08-23 15:00);
let max_peak_t=datetime(2016-08-23 15:02);
demo_clustering1
| where PreciseTimeStamp between(min_peak_t..max_peak_t)
| evaluate autocluster()
| SegmentId | Count | Percent | Region | ScaleUnit | DeploymentId | ServiceHost |
|---|---|---|---|---|---|---|
| 0 | 639 | 65.7407407407407 | eau | su7 | b5d1d4df547d4a04ac15885617edba57 | e7f60c5d-4944-42b3-922a-92e98a8e7dec |
| 1 | 94 | 9.67078189300411 | scus | su5 | 9dbd1b161d5b4779a73cf19a7836ebd6 | |
| 2 | 82 | 8.43621399176955 | ncus | su1 | e24ef436e02b4823ac5d5b1465a9401e | |
| 3 | 68 | 6.99588477366255 | scus | su3 | 90d3d2fc7ecc430c9621ece335651a01 | |
| 4 | 55 | 5.65843621399177 | weu | su4 | be1d6d7ac9574cbc9a22cb8ee20f16fc |
You can see from the results above that the most dominant segment contains 65.74% of the total exception records and shares four dimensions. The next segment is much less common. It contains only 9.67% of the records, and shares three dimensions. The other segments are even less common.
Autocluster uses a proprietary algorithm for mining multiple dimensions and extracting interesting segments. “Interesting” means that each segment has significant coverage of both the records set and the features set. The segments are also diverged, meaning that each one is different from the others. One or more of these segments might be relevant for the RCA process. To minimize segment review and assessment, autocluster extracts only a small segment list.
You can also use the basket() plugin as seen in the following query:
let min_peak_t=datetime(2016-08-23 15:00);
let max_peak_t=datetime(2016-08-23 15:02);
demo_clustering1
| where PreciseTimeStamp between(min_peak_t..max_peak_t)
| evaluate basket()
| SegmentId | Count | Percent | Region | ScaleUnit | DeploymentId | Tracepoint | ServiceHost |
|---|---|---|---|---|---|---|---|
| 0 | 639 | 65.7407407407407 | eau | su7 | b5d1d4df547d4a04ac15885617edba57 | e7f60c5d-4944-42b3-922a-92e98a8e7dec | |
| 1 | 642 | 66.0493827160494 | eau | su7 | b5d1d4df547d4a04ac15885617edba57 | ||
| 2 | 324 | 33.3333333333333 | eau | su7 | b5d1d4df547d4a04ac15885617edba57 | 0 | e7f60c5d-4944-42b3-922a-92e98a8e7dec |
| 3 | 315 | 32.4074074074074 | eau | su7 | b5d1d4df547d4a04ac15885617edba57 | 16108 | e7f60c5d-4944-42b3-922a-92e98a8e7dec |
| 4 | 328 | 33.7448559670782 | 0 | ||||
| 5 | 94 | 9.67078189300411 | scus | su5 | 9dbd1b161d5b4779a73cf19a7836ebd6 | ||
| 6 | 82 | 8.43621399176955 | ncus | su1 | e24ef436e02b4823ac5d5b1465a9401e | ||
| 7 | 68 | 6.99588477366255 | scus | su3 | 90d3d2fc7ecc430c9621ece335651a01 | ||
| 8 | 167 | 17.1810699588477 | scus | ||||
| 9 | 55 | 5.65843621399177 | weu | su4 | be1d6d7ac9574cbc9a22cb8ee20f16fc | ||
| 10 | 92 | 9.46502057613169 | 10007007 | ||||
| 11 | 90 | 9.25925925925926 | 10007006 | ||||
| 12 | 57 | 5.8641975308642 | 00000000-0000-0000-0000-000000000000 |
Basket implements the “Apriori” algorithm for item set mining. It extracts all segments whose coverage of the record set is above a threshold (default 5%). You can see that more segments were extracted with similar ones, such as segments 0, 1 or 2, 3.
Both plugins are powerful and easy to use. Their limitation is that they cluster a single record set in an unsupervised manner with no labels. It’s unclear whether the extracted patterns characterize the selected record set, anomalous records, or the global record set.
Clustering the difference between two records sets
The diffpatterns() plugin overcomes the limitation of autocluster and basket. Diffpatterns takes two record sets and extracts the main segments that are different. One set usually contains the anomalous record set being investigated. One is analyzed by autocluster and basket. The other set contains the reference record set, the baseline.
In the following query, diffpatterns finds interesting clusters within the spike’s two minutes, which are different from the clusters within the baseline. The baseline window is defined as the eight minutes before 15:00, when the spike started. You extend by a binary column (AB), and specify whether a specific record belongs to the baseline or to the anomalous set. Diffpatterns implements a supervised learning algorithm, where the two class labels were generated by the anomalous versus the baseline flag (AB).
let min_peak_t=datetime(2016-08-23 15:00);
let max_peak_t=datetime(2016-08-23 15:02);
let min_baseline_t=datetime(2016-08-23 14:50);
let max_baseline_t=datetime(2016-08-23 14:58); // Leave a gap between the baseline and the spike to avoid the transition zone.
let splitime=(max_baseline_t+min_peak_t)/2.0;
demo_clustering1
| where (PreciseTimeStamp between(min_baseline_t..max_baseline_t)) or
(PreciseTimeStamp between(min_peak_t..max_peak_t))
| extend AB=iff(PreciseTimeStamp > splitime, 'Anomaly', 'Baseline')
| evaluate diffpatterns(AB, 'Anomaly', 'Baseline')
| SegmentId | CountA | CountB | PercentA | PercentB | PercentDiffAB | Region | ScaleUnit | DeploymentId | Tracepoint |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 639 | 21 | 65.74 | 1.7 | 64.04 | eau | su7 | b5d1d4df547d4a04ac15885617edba57 | |
| 1 | 167 | 544 | 17.18 | 44.16 | 26.97 | scus | |||
| 2 | 92 | 356 | 9.47 | 28.9 | 19.43 | 10007007 | |||
| 3 | 90 | 336 | 9.26 | 27.27 | 18.01 | 10007006 | |||
| 4 | 82 | 318 | 8.44 | 25.81 | 17.38 | ncus | su1 | e24ef436e02b4823ac5d5b1465a9401e | |
| 5 | 55 | 252 | 5.66 | 20.45 | 14.8 | weu | su4 | be1d6d7ac9574cbc9a22cb8ee20f16fc | |
| 6 | 57 | 204 | 5.86 | 16.56 | 10.69 |
The most dominant segment is the same segment that was extracted by autocluster. Its coverage on the two-minute anomalous window is also 65.74%. However, its coverage on the eight-minute baseline window is only 1.7%. The difference is 64.04%. This difference seems to be related to the anomalous spike. To verify this assumption, the following query splits the original chart into the records that belong to this problematic segment, and records from the other segments.
let min_t = toscalar(demo_clustering1 | summarize min(PreciseTimeStamp));
let max_t = toscalar(demo_clustering1 | summarize max(PreciseTimeStamp));
demo_clustering1
| extend seg = iff(Region == "eau" and ScaleUnit == "su7" and DeploymentId == "b5d1d4df547d4a04ac15885617edba57"
and ServiceHost == "e7f60c5d-4944-42b3-922a-92e98a8e7dec", "Problem", "Normal")
| make-series num=count() on PreciseTimeStamp from min_t to max_t step 10m by seg
| render timechart

This chart allows us to see that the spike on Tuesday afternoon was because of exceptions from this specific segment, discovered by using the diffpatterns plugin.
Summary
The Machine Learning plugins are helpful for many scenarios. The autocluster and basket implement an unsupervised learning algorithm and are easy to use. Diffpatterns implements a supervised learning algorithm and, although more complex, it’s more powerful for extracting differentiation segments for RCA.
These plugins are used interactively in ad-hoc scenarios and in automatic near real-time monitoring services. Time series anomaly detection is followed by a diagnosis process. The process is highly optimized to meet necessary performance standards.
1.3 - Time series anomaly detection & forecasting
Cloud services and IoT devices generate telemetry you use to monitor service health, production processes, and usage trends. Time series analysis helps you spot deviations from each metric’s baseline pattern.
Kusto Query Language (KQL) includes native support for creating, manipulating, and analyzing multiple time series. Use KQL to create and analyze thousands of time series in seconds for near real time monitoring.
This article describes KQL time series anomaly detection and forecasting capabilities. The functions use a robust, well known decomposition model that splits each time series into seasonal, trend, and residual components. Detect anomalies by finding outliers in the residual component. Forecast by extrapolating the seasonal and trend components. KQL adds automatic seasonality detection, robust outlier analysis, and a vectorized implementation that processes thousands of time series in seconds.
Prerequisites
- Use a Microsoft account or a Microsoft Entra user identity. You don’t need an Azure subscription.
- Read about time series capabilities in Time series analysis.
Time series decomposition model
The KQL native implementation for time series prediction and anomaly detection uses a well known decomposition model. Use this model for time series with periodic and trend behavior—like service traffic, component heartbeats, and periodic IoT measurements—to forecast future values and detect anomalies. The regression assumes the remainder is random after removing the seasonal and trend components. Forecast future values from the seasonal and trend components (the baseline) and ignore the residual. Detect anomalies by running outlier analysis on the residual component.
Use the series_decompose() function to create a decomposition model. It decomposes each time series into seasonal, trend, residual, and baseline components.
Example: Decompose internal web service traffic:
let min_t = datetime(2017-01-05);
let max_t = datetime(2017-02-03 22:00);
let dt = 2h;
demo_make_series2
| make-series num=avg(num) on TimeStamp from min_t to max_t step dt by sid
| where sid == 'TS1' // Select a single time series for cleaner visualization
| extend (baseline, seasonal, trend, residual) = series_decompose(num, -1, 'linefit') // Decompose each time series into seasonal, trend, residual, and baseline (seasonal + trend)
| render timechart with(title='Web app traffic for one month, decomposition', ysplit=panels)

- The original time series is labeled num (in red).
- The process autodetects seasonality using the
series_periods_detect()function and extracts the seasonal pattern (purple). - Subtract the seasonal pattern from the original time series, then run a linear regression with the
series_fit_line()function to find the trend component (light blue). - The function subtracts the trend, and the remainder is the residual component (green).
- Finally, add the seasonal and trend components to generate the baseline (blue).
Time series anomaly detection
The function series_decompose_anomalies() finds anomalous points on a set of time series. This function calls series_decompose() to build the decomposition model and then runs series_outliers() on the residual component. series_outliers() calculates anomaly scores for each point of the residual component using Tukey’s fence test. Anomaly scores above 1.5 or below -1.5 indicate a mild anomaly rise or decline respectively. Anomaly scores above 3.0 or below -3.0 indicate a strong anomaly.
The following query allows you to detect anomalies in internal web service traffic:
let min_t = datetime(2017-01-05);
let max_t = datetime(2017-02-03 22:00);
let dt = 2h;
demo_make_series2
| make-series num=avg(num) on TimeStamp from min_t to max_t step dt by sid
| where sid == 'TS1' // select a single time series for a cleaner visualization
| extend (anomalies, score, baseline) = series_decompose_anomalies(num, 1.5, -1, 'linefit')
| render anomalychart with(anomalycolumns=anomalies, title='Web app. traffic of a month, anomalies') //use "| render anomalychart with anomalycolumns=anomalies" to render the anomalies as bold points on the series charts.

- The original time series (in red).
- The baseline (seasonal + trend) component (in blue).
- The anomalous points (in purple) on top of the original time series. The anomalous points significantly deviate from the expected baseline values.
Time series forecasting
The function series_decompose_forecast() predicts future values of a set of time series. This function calls series_decompose() to build the decomposition model and then, for each time series, extrapolates the baseline component into the future.
The following query allows you to predict next week’s web service traffic:
let min_t = datetime(2017-01-05);
let max_t = datetime(2017-02-03 22:00);
let dt = 2h;
let horizon=7d;
demo_make_series2
| make-series num=avg(num) on TimeStamp from min_t to max_t+horizon step dt by sid
| where sid == 'TS1' // select a single time series for a cleaner visualization
| extend forecast = series_decompose_forecast(num, toint(horizon/dt))
| render timechart with(title='Web app. traffic of a month, forecasting the next week by Time Series Decomposition')

- Original metric (in red). Future values are missing and set to 0, by default.
- Extrapolate the baseline component (in blue) to predict next week’s values.
Scalability
Kusto Query Language syntax enables a single call to process multiple time series. Its unique optimized implementation allows for fast performance, which is critical for effective anomaly detection and forecasting when monitoring thousands of counters in near real-time scenarios.
The following query shows the processing of three time series simultaneously:
let min_t = datetime(2017-01-05);
let max_t = datetime(2017-02-03 22:00);
let dt = 2h;
let horizon=7d;
demo_make_series2
| make-series num=avg(num) on TimeStamp from min_t to max_t+horizon step dt by sid
| extend offset=case(sid=='TS3', 4000000, sid=='TS2', 2000000, 0) // add artificial offset for easy visualization of multiple time series
| extend num=series_add(num, offset)
| extend forecast = series_decompose_forecast(num, toint(horizon/dt))
| render timechart with(title='Web app. traffic of a month, forecasting the next week for 3 time series')

Summary
This document details native KQL functions for time series anomaly detection and forecasting. Each original time series is decomposed into seasonal, trend, and residual components for detecting anomalies and/or forecasting. These functionalities can be used for near real-time monitoring scenarios, such as fault detection, predictive maintenance, and demand and load forecasting.
Related content
- Learn about Anomaly diagnosis capabilities with KQL
2 - series_product()
Calculates the product of series elements.
Syntax
series_product(series)
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| series | dynamic | ✔️ | Array of numeric values. |
Returns
Returns a double type value with the product of the elements of the array.
Example
print arr=dynamic([1,2,3,4])
| extend series_product=series_product(arr)
Output
| s1 | series_product |
|---|---|
| [1,2,3,4] | 24 |
3 - make-series operator
Create series of specified aggregated values along a specified axis.
Syntax
T | make-series [MakeSeriesParameters]
[Column =] Aggregation [default = DefaultValue] [, …]
on AxisColumn [from start] [to end] step step
[by
[Column =] GroupExpression [, …]]
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| Column | string | The name for the result column. Defaults to a name derived from the expression. | |
| DefaultValue | scalar | A default value to use instead of absent values. If there’s no row with specific values of AxisColumn and GroupExpression, then the corresponding element of the array is assigned a DefaultValue. Default is 0. | |
| Aggregation | string | ✔️ | A call to an aggregation function, such as count() or avg(), with column names as arguments. See the list of aggregation functions. Only aggregation functions that return numeric results can be used with the make-series operator. |
| AxisColumn | string | ✔️ | The column by which the series is ordered. Usually the column values are of type datetime or timespan but all numeric types are accepted. |
| start | scalar | ✔️ | The low bound value of the AxisColumn for each of the series to be built. If start isn’t specified, it’s the first bin, or step, that has data in each series. |
| end | scalar | ✔️ | The high bound non-inclusive value of the AxisColumn. The last index of the time series is smaller than this value and is start plus integer multiple of step that is smaller than end. If end isn’t specified, it’s the upper bound of the last bin, or step, that has data per each series. |
| step | scalar | ✔️ | The difference, or bin size, between two consecutive elements of the AxisColumn array. For a list of possible time intervals, see timespan. |
| GroupExpression | An expression over the columns that provides a set of distinct values. Typically it’s a column name that already provides a restricted set of values. | ||
| MakeSeriesParameters | Zero or more space-separated parameters in the form of Name = Value that control the behavior. See supported make series parameters. |
Supported make series parameters
| Name | Description |
|---|---|
kind | Produces default result when the input of make-series operator is empty. Value: nonempty |
hint.shufflekey=<key> | The shufflekey query shares the query load on cluster nodes, using a key to partition data. See shuffle query |
Alternate Syntax
T | make-series
[Column =] Aggregation [default = DefaultValue] [, …]
on AxisColumn in range(start, stop, step)
[by
[Column =] GroupExpression [, …]]
The generated series from the alternate syntax differs from the main syntax in two aspects:
- The stop value is inclusive.
- Binning the index axis is generated with bin() and not bin_at(), which means that start might not be included in the generated series.
We recommend that you use the main syntax of make-series and not the alternate syntax.
Returns
The input rows are arranged into groups having the same values of the by expressions and the bin_at(AxisColumn,step,start) expression. Then the specified aggregation functions are computed over each group, producing a row for each group. The result contains the by columns, AxisColumn column and also at least one column for each computed aggregate. (Aggregations over multiple columns or non-numeric results aren’t supported.)
This intermediate result has as many rows as there are distinct combinations of by and bin_at(AxisColumn,step,start) values.
Finally the rows from the intermediate result arranged into groups having the same values of the by expressions and all aggregated values are arranged into arrays (values of dynamic type). For each aggregation, there’s one column containing its array with the same name. The last column is an array containing the values of AxisColumn binned according to the specified step.
List of aggregation functions
| Function | Description |
|---|---|
| avg() | Returns an average value across the group |
| avgif() | Returns an average with the predicate of the group |
| count() | Returns a count of the group |
| countif() | Returns a count with the predicate of the group |
| covariance() | Returns the sample covariance of two random variables |
| covarianceif() | Returns the sample covariance of two random variables with predicate |
| covariancep() | Returns the population covariance of two random variables |
| covariancepif() | Returns the population covariance of two random variables with predicate |
| dcount() | Returns an approximate distinct count of the group elements |
| dcountif() | Returns an approximate distinct count with the predicate of the group |
| max() | Returns the maximum value across the group |
| maxif() | Returns the maximum value with the predicate of the group |
| min() | Returns the minimum value across the group |
| minif() | Returns the minimum value with the predicate of the group |
| percentile() | Returns the percentile value across the group |
| take_any() | Returns a random non-empty value for the group |
| stdev() | Returns the standard deviation across the group |
| sum() | Returns the sum of the elements within the group |
| sumif() | Returns the sum of the elements with the predicate of the group |
| variance() | Returns the sample variance across the group |
| varianceif() | Returns the sample variance across the group with predicate |
| variancep() | Returns the population variance across the group |
| variancepif() | Returns the population variance across the group with predicate |
List of series analysis functions
| Function | Description |
|---|---|
| series_fir() | Applies Finite Impulse Response filter |
| series_iir() | Applies Infinite Impulse Response filter |
| series_fit_line() | Finds a straight line that is the best approximation of the input |
| series_fit_line_dynamic() | Finds a line that is the best approximation of the input, returning dynamic object |
| series_fit_2lines() | Finds two lines that are the best approximation of the input |
| series_fit_2lines_dynamic() | Finds two lines that are the best approximation of the input, returning dynamic object |
| series_outliers() | Scores anomaly points in a series |
| series_periods_detect() | Finds the most significant periods that exist in a time series |
| series_periods_validate() | Checks whether a time series contains periodic patterns of given lengths |
| series_stats_dynamic() | Return multiple columns with the common statistics (min/max/variance/stdev/average) |
| series_stats() | Generates a dynamic value with the common statistics (min/max/variance/stdev/average) |
For a complete list of series analysis functions, see: Series processing functions
List of series interpolation functions
| Function | Description |
|---|---|
| series_fill_backward() | Performs backward fill interpolation of missing values in a series |
| series_fill_const() | Replaces missing values in a series with a specified constant value |
| series_fill_forward() | Performs forward fill interpolation of missing values in a series |
| series_fill_linear() | Performs linear interpolation of missing values in a series |
- Note: Interpolation functions by default assume
nullas a missing value. Therefore specifydefault=double(null) inmake-seriesif you intend to use interpolation functions for the series.
Examples
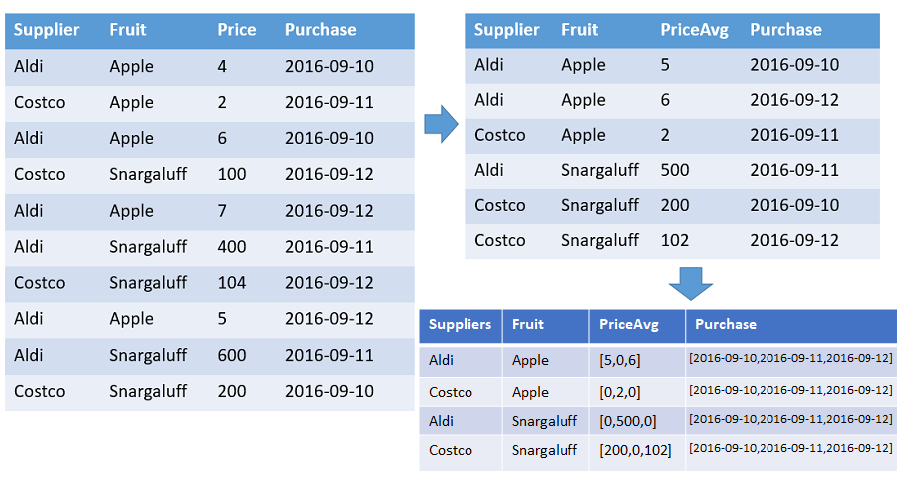
A table that shows arrays of the numbers and average prices of each fruit from each supplier ordered by the timestamp with specified range. There’s a row in the output for each distinct combination of fruit and supplier. The output columns show the fruit, supplier, and arrays of: count, average, and the whole timeline (from 2016-01-01 until 2016-01-10). All arrays are sorted by the respective timestamp and all gaps are filled with default values (0 in this example). All other input columns are ignored.
T | make-series PriceAvg=avg(Price) default=0
on Purchase from datetime(2016-09-10) to datetime(2016-09-13) step 1d by Supplier, Fruit
let data=datatable(timestamp:datetime, metric: real)
[
datetime(2016-12-31T06:00), 50,
datetime(2017-01-01), 4,
datetime(2017-01-02), 3,
datetime(2017-01-03), 4,
datetime(2017-01-03T03:00), 6,
datetime(2017-01-05), 8,
datetime(2017-01-05T13:40), 13,
datetime(2017-01-06), 4,
datetime(2017-01-07), 3,
datetime(2017-01-08), 8,
datetime(2017-01-08T21:00), 8,
datetime(2017-01-09), 2,
datetime(2017-01-09T12:00), 11,
datetime(2017-01-10T05:00), 5,
];
let interval = 1d;
let stime = datetime(2017-01-01);
let etime = datetime(2017-01-10);
data
| make-series avg(metric) on timestamp from stime to etime step interval
| avg_metric | timestamp |
|---|---|
| [ 4.0, 3.0, 5.0, 0.0, 10.5, 4.0, 3.0, 8.0, 6.5 ] | [ “2017-01-01T00:00:00.0000000Z”, “2017-01-02T00:00:00.0000000Z”, “2017-01-03T00:00:00.0000000Z”, “2017-01-04T00:00:00.0000000Z”, “2017-01-05T00:00:00.0000000Z”, “2017-01-06T00:00:00.0000000Z”, “2017-01-07T00:00:00.0000000Z”, “2017-01-08T00:00:00.0000000Z”, “2017-01-09T00:00:00.0000000Z” ] |
When the input to make-series is empty, the default behavior of make-series produces an empty result.
let data=datatable(timestamp:datetime, metric: real)
[
datetime(2016-12-31T06:00), 50,
datetime(2017-01-01), 4,
datetime(2017-01-02), 3,
datetime(2017-01-03), 4,
datetime(2017-01-03T03:00), 6,
datetime(2017-01-05), 8,
datetime(2017-01-05T13:40), 13,
datetime(2017-01-06), 4,
datetime(2017-01-07), 3,
datetime(2017-01-08), 8,
datetime(2017-01-08T21:00), 8,
datetime(2017-01-09), 2,
datetime(2017-01-09T12:00), 11,
datetime(2017-01-10T05:00), 5,
];
let interval = 1d;
let stime = datetime(2017-01-01);
let etime = datetime(2017-01-10);
data
| take 0
| make-series avg(metric) default=1.0 on timestamp from stime to etime step interval
| count
Output
| Count |
|---|
| 0 |
Using kind=nonempty in make-series produces a non-empty result of the default values:
let data=datatable(timestamp:datetime, metric: real)
[
datetime(2016-12-31T06:00), 50,
datetime(2017-01-01), 4,
datetime(2017-01-02), 3,
datetime(2017-01-03), 4,
datetime(2017-01-03T03:00), 6,
datetime(2017-01-05), 8,
datetime(2017-01-05T13:40), 13,
datetime(2017-01-06), 4,
datetime(2017-01-07), 3,
datetime(2017-01-08), 8,
datetime(2017-01-08T21:00), 8,
datetime(2017-01-09), 2,
datetime(2017-01-09T12:00), 11,
datetime(2017-01-10T05:00), 5,
];
let interval = 1d;
let stime = datetime(2017-01-01);
let etime = datetime(2017-01-10);
data
| take 0
| make-series kind=nonempty avg(metric) default=1.0 on timestamp from stime to etime step interval
Output
| avg_metric | timestamp |
|---|---|
| [ 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0 ] | [ “2017-01-01T00:00:00.0000000Z”, “2017-01-02T00:00:00.0000000Z”, “2017-01-03T00:00:00.0000000Z”, “2017-01-04T00:00:00.0000000Z”, “2017-01-05T00:00:00.0000000Z”, “2017-01-06T00:00:00.0000000Z”, “2017-01-07T00:00:00.0000000Z”, “2017-01-08T00:00:00.0000000Z”, “2017-01-09T00:00:00.0000000Z” ] |
Using make-series and mv-expand to fill values for missing records:
let startDate = datetime(2025-01-06);
let endDate = datetime(2025-02-09);
let data = datatable(Time: datetime, Value: int, other:int)
[
datetime(2025-01-07), 10, 11,
datetime(2025-01-16), 20, 21,
datetime(2025-02-01), 30, 5
];
data
| make-series Value=sum(Value), other=-1 default=-2 on Time from startDate to endDate step 7d
| mv-expand Value, Time, other
| extend Time=todatetime(Time), Value=toint(Value), other=toint(other)
| project-reorder Time, Value, other
Output
| Time | Value | other |
|---|---|---|
| 2025-01-06T00:00:00Z | 10 | -1 |
| 2025-01-13T00:00:00Z | 20 | -1 |
| 2025-01-20T00:00:00Z | 0 | -2 |
| 2025-01-27T00:00:00Z | 30 | -1 |
| 2025-02-03T00:00:00Z | 0 | -2 |
|2025-02-03T00:00:00Z|0|-2|
4 - series_abs()
Calculates the element-wise absolute value of the numeric series input.
Syntax
series_abs(series)
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| series | dynamic | ✔️ | An array of numeric values over which the absolute value function is applied. |
Returns
Dynamic array of calculated absolute value. Any non-numeric element yields a null element value.
Example
print arr = dynamic([-6.5,0,8.2])
| extend arr_abs = series_abs(arr)
Output
| arr | arr_abs |
|---|---|
| [-6.5,0,8.2] | [6.5,0,8.2] |
5 - series_acos()
Calculates the element-wise arccosine function of the numeric series input.
Syntax
series_acos(series)
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| series | dynamic | ✔️ | An array of numeric values over which the arccosine function is applied. |
Returns
Dynamic array of calculated arccosine function values. Any non-numeric element yields a null element value.
Example
print arr = dynamic([-1,0,1])
| extend arr_acos = series_acos(arr)
Output
| arr | arr_acos |
|---|---|
| [-6.5,0,8.2] | [3.1415926535897931,1.5707963267948966,0.0] |
6 - series_add()
Calculates the element-wise addition of two numeric series inputs.
Syntax
series_add(series1, series2)
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| series1, series2 | dynamic | ✔️ | The numeric arrays to be element-wise added into a dynamic array result. |
Returns
Dynamic array of calculated element-wise add operation between the two inputs. Any non-numeric element or non-existing element (arrays of different sizes) yields a null element value.
Example
range x from 1 to 3 step 1
| extend y = x * 2
| extend z = y * 2
| project s1 = pack_array(x,y,z), s2 = pack_array(z, y, x)
| extend s1_add_s2 = series_add(s1, s2)
Output
| s1 | s2 | s1_add_s2 |
|---|---|---|
| [1,2,4] | [4,2,1] | [5,4,5] |
| [2,4,8] | [8,4,2] | [10,8,10] |
| [3,6,12] | [12,6,3] | [15,12,15] |
7 - series_atan()
Calculates the element-wise arctangent function of the numeric series input.
Syntax
series_atan(series)
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| series | dynamic | ✔️ | An array of numeric values over which the arctangent function is applied. |
Returns
Dynamic array of calculated arctangent function values. Any non-numeric element yields a null element value.
Example
print arr = dynamic([-1,0,1])
| extend arr_atan = series_atan(arr)
Output
| arr | arr_atan |
|---|---|
| [-6.5,0,8.2] | [-0.78539816339744828,0.0,0.78539816339744828] |
8 - series_cos()
Calculates the element-wise cosine function of the numeric series input.
Syntax
series_cos(series)
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| series | dynamic | ✔️ | An array of numeric values over which the cosine function is applied. |
Returns
Dynamic array of calculated cosine function values. Any non-numeric element yields a null element value.
Example
print arr = dynamic([-1,0,1])
| extend arr_cos = series_cos(arr)
Output
| arr | arr_cos |
|---|---|
| [-6.5,0,8.2] | [0.54030230586813976,1.0,0.54030230586813976] |
9 - series_cosine_similarity()
Calculate the cosine similarity of two numerical vectors.
The function series_cosine_similarity() takes two numeric series as input, and calculates their cosine similarity.
Syntax
series_cosine_similarity(series1, series2, [*magnitude1, [*magnitude2]])
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| series1, series2 | dynamic | ✔️ | Input arrays with numeric data. |
| magnitude1, magnitude2 | real | Optional magnitude of the first and the second vectors respectively. The magnitude is the square root of the dot product of the vector with itself. If the magnitude isn’t provided, it will be calculated. |
Returns
Returns a value of type real whose value is the cosine similarity of series1 with series2.
In case both series length isn’t equal, the longer series will be truncated to the length of the shorter one.
Any non-numeric element of the input series will be ignored.
Example
target="_blank">Run the query
datatable(s1:dynamic, s2:dynamic)
[
dynamic([0.1,0.2,0.1,0.2]), dynamic([0.11,0.2,0.11,0.21]),
dynamic([0.1,0.2,0.1,0.2]), dynamic([1,2,3,4]),
]
| extend cosine_similarity=series_cosine_similarity(s1, s2)
| s1 | s2 | cosine_similarity |
|---|---|---|
| [0.1,0.2,0.1,0.2] | [0.11,0.2,0.11,0.21] | 0.99935343825504 |
| [0.1,0.2,0.1,0.2] | [1,2,3,4] | 0.923760430703401 |
Related content
10 - series_decompose_anomalies()
Anomaly Detection is based on series decomposition. For more information, see series_decompose().
The function takes an expression containing a series (dynamic numerical array) as input, and extracts anomalous points with scores.
Syntax
series_decompose_anomalies (Series, [ Threshold, Seasonality, Trend, Test_points, AD_method, Seasonality_threshold ])
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| Series | dynamic | ✔️ | An array of numeric values, typically the resulting output of make-series or make_list operators. |
| Threshold | real | The anomaly threshold. The default is 1.5, k value, for detecting mild or stronger anomalies. | |
| Seasonality | int | Controls the seasonal analysis. The possible values are: - -1: Autodetect seasonality using series_periods_detect. This is the default value.- Integer time period: A positive integer specifying the expected period in number of bins. For example, if the series is in 1h bins, a weekly period is 168 bins.- 0: No seasonality, so skip extracting this component. | |
| Trend | string | Controls the trend analysis. The possible values are: - avg: Define trend component as average(x). This is the default.- linefit: Extract trend component using linear regression.- none: No trend, so skip extracting this component. | |
| Test_points | int | A positive integer specifying the number of points at the end of the series to exclude from the learning, or regression, process. This parameter should be set for forecasting purposes. The default value is 0. | |
| AD_method | string | Controls the anomaly detection method on the residual time series, containing one of the following values: - ctukey: Tukey’s fence test with custom 10th-90th percentile range. This is the default.- tukey: Tukey’s fence test with standard 25th-75th percentile range.For more information on residual time series, see series_outliers. | |
| Seasonality_threshold | real | The threshold for seasonality score when Seasonality is set to autodetect. The default score threshold is 0.6. For more information, see series_periods_detect. |
Returns
The function returns the following respective series:
ad_flag: A ternary series containing (+1, -1, 0) marking up/down/no anomaly respectivelyad_score: Anomaly scorebaseline: The predicted value of the series, according to the decomposition
The algorithm
This function follows these steps:
- Calls series_decompose() with the respective parameters, to create the baseline and residuals series.
- Calculates ad_score series by applying series_outliers() with the chosen anomaly detection method on the residuals series.
- Calculates the ad_flag series by applying the threshold on the ad_score to mark up/down/no anomaly respectively.
Examples
Detect anomalies in weekly seasonality
In the following example, generate a series with weekly seasonality, and then add some outliers to it. series_decompose_anomalies autodetects the seasonality and generates a baseline that captures the repetitive pattern. The outliers you added can be clearly spotted in the ad_score component.
let ts=range t from 1 to 24*7*5 step 1
| extend Timestamp = datetime(2018-03-01 05:00) + 1h * t
| extend y = 2*rand() + iff((t/24)%7>=5, 10.0, 15.0) - (((t%24)/10)*((t%24)/10)) // generate a series with weekly seasonality
| extend y=iff(t==150 or t==200 or t==780, y-8.0, y) // add some dip outliers
| extend y=iff(t==300 or t==400 or t==600, y+8.0, y) // add some spike outliers
| summarize Timestamp=make_list(Timestamp, 10000),y=make_list(y, 10000);
ts
| extend series_decompose_anomalies(y)
| render timechart
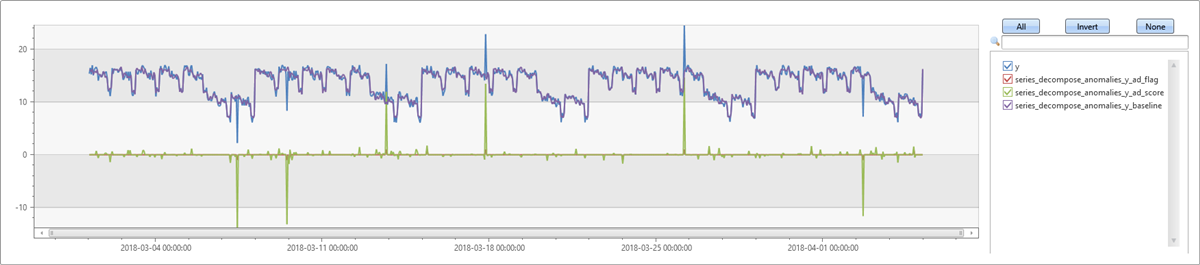
Detect anomalies in weekly seasonality with trend
In this example, add a trend to the series from the previous example. First, run series_decompose_anomalies with the default parameters in which the trend avg default value only takes the average and doesn’t compute the trend. The generated baseline doesn’t contain the trend and is less exact, compared to the previous example. Consequently, some of the outliers you inserted in the data aren’t detected because of the higher variance.
let ts=range t from 1 to 24*7*5 step 1
| extend Timestamp = datetime(2018-03-01 05:00) + 1h * t
| extend y = 2*rand() + iff((t/24)%7>=5, 5.0, 15.0) - (((t%24)/10)*((t%24)/10)) + t/72.0 // generate a series with weekly seasonality and ongoing trend
| extend y=iff(t==150 or t==200 or t==780, y-8.0, y) // add some dip outliers
| extend y=iff(t==300 or t==400 or t==600, y+8.0, y) // add some spike outliers
| summarize Timestamp=make_list(Timestamp, 10000),y=make_list(y, 10000);
ts
| extend series_decompose_anomalies(y)
| extend series_decompose_anomalies_y_ad_flag =
series_multiply(10, series_decompose_anomalies_y_ad_flag) // multiply by 10 for visualization purposes
| render timechart
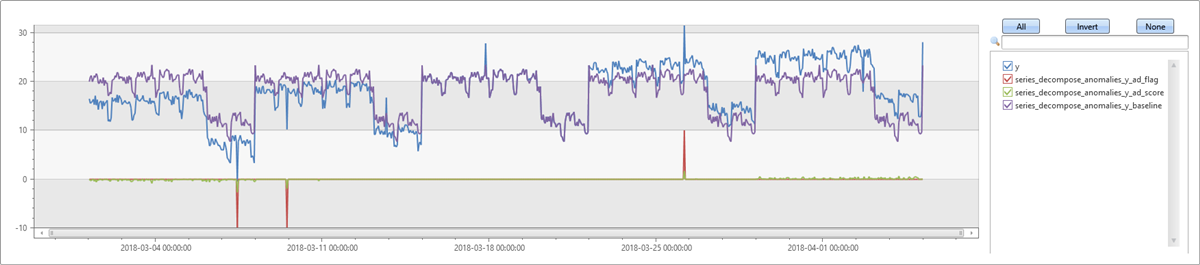
Next, run the same example, but since you’re expecting a trend in the series, specify linefit in the trend parameter. You can see that the baseline is much closer to the input series. All the inserted outliers are detected, and also some false positives. See the next example on tweaking the threshold.
let ts=range t from 1 to 24*7*5 step 1
| extend Timestamp = datetime(2018-03-01 05:00) + 1h * t
| extend y = 2*rand() + iff((t/24)%7>=5, 5.0, 15.0) - (((t%24)/10)*((t%24)/10)) + t/72.0 // generate a series with weekly seasonality and ongoing trend
| extend y=iff(t==150 or t==200 or t==780, y-8.0, y) // add some dip outliers
| extend y=iff(t==300 or t==400 or t==600, y+8.0, y) // add some spike outliers
| summarize Timestamp=make_list(Timestamp, 10000),y=make_list(y, 10000);
ts
| extend series_decompose_anomalies(y, 1.5, -1, 'linefit')
| extend series_decompose_anomalies_y_ad_flag =
series_multiply(10, series_decompose_anomalies_y_ad_flag) // multiply by 10 for visualization purposes
| render timechart
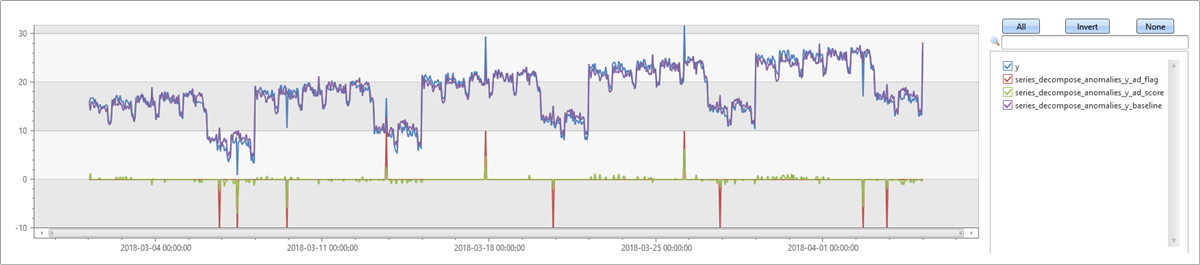
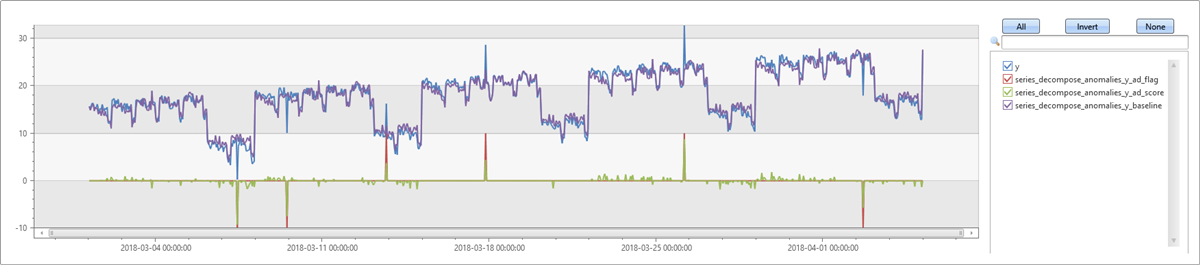
Tweak the anomaly detection threshold
A few noisy points were detected as anomalies in the previous example. Now increase the anomaly detection threshold from a default of 1.5 to 2.5. Use this interpercentile range, so that only stronger anomalies are detected. Now, only the outliers you inserted in the data, will be detected.
let ts=range t from 1 to 24*7*5 step 1
| extend Timestamp = datetime(2018-03-01 05:00) + 1h * t
| extend y = 2*rand() + iff((t/24)%7>=5, 5.0, 15.0) - (((t%24)/10)*((t%24)/10)) + t/72.0 // generate a series with weekly seasonality and onlgoing trend
| extend y=iff(t==150 or t==200 or t==780, y-8.0, y) // add some dip outliers
| extend y=iff(t==300 or t==400 or t==600, y+8.0, y) // add some spike outliers
| summarize Timestamp=make_list(Timestamp, 10000),y=make_list(y, 10000);
ts
| extend series_decompose_anomalies(y, 2.5, -1, 'linefit')
| extend series_decompose_anomalies_y_ad_flag =
series_multiply(10, series_decompose_anomalies_y_ad_flag) // multiply by 10 for visualization purposes
| render timechart
11 - series_decompose_forecast()
Forecast based on series decomposition.
Takes an expression containing a series (dynamic numerical array) as input, and predicts the values of the last trailing points. For more information, see series_decompose.
Syntax
series_decompose_forecast(Series, Points, [ Seasonality, Trend, Seasonality_threshold ])
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| Series | dynamic | ✔️ | An array of numeric values, typically the resulting output of make-series or make_list operators. |
| Points | int | ✔️ | Specifies the number of points at the end of the series to predict, or forecast. These points are excluded from the learning, or regression, process. |
| Seasonality | int | Controls the seasonal analysis. The possible values are: - -1: Autodetect seasonality using series_periods_detect. This is the default value.- Period: A positive integer specifying the expected period in number of bins. For example, if the series is in 1 - h bins, a weekly period is 168 bins.- 0: No seasonality, so skip extracting this component. | |
| Trend | string | Controls the trend analysis. The possible values are: - avg: Define trend component as average(x). This is the default.- linefit: Extract trend component using linear regression.- none: No trend, so skip extracting this component. | |
| Seasonality_threshold | real | The threshold for seasonality score when Seasonality is set to autodetect. The default score threshold is 0.6. For more information, see series_periods_detect. |
Returns
A dynamic array with the forecasted series.
Example
In the following example, we generate a series of four weeks in an hourly grain, with weekly seasonality and a small upward trend. We then use make-series and add another empty week to the series. series_decompose_forecast is called with a week (24*7 points), and it automatically detects the seasonality and trend, and generates a forecast of the entire five-week period.
let ts=range t from 1 to 24*7*4 step 1 // generate 4 weeks of hourly data
| extend Timestamp = datetime(2018-03-01 05:00) + 1h * t
| extend y = 2*rand() + iff((t/24)%7>=5, 5.0, 15.0) - (((t%24)/10)*((t%24)/10)) + t/72.0 // generate a series with weekly seasonality and ongoing trend
| extend y=iff(t==150 or t==200 or t==780, y-8.0, y) // add some dip outliers
| extend y=iff(t==300 or t==400 or t==600, y+8.0, y) // add some spike outliers
| make-series y=max(y) on Timestamp from datetime(2018-03-01 05:00) to datetime(2018-03-01 05:00)+24*7*5h step 1h; // create a time series of 5 weeks (last week is empty)
ts
| extend y_forcasted = series_decompose_forecast(y, 24*7) // forecast a week forward
| render timechart

12 - series_decompose()
Applies a decomposition transformation on a series.
Takes an expression containing a series (dynamic numerical array) as input and decomposes it to seasonal, trend, and residual components.
Syntax
series_decompose(Series , [ Seasonality, Trend, Test_points, Seasonality_threshold ])
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| Series | dynamic | ✔️ | An array of numeric values, typically the resulting output of make-series or make_list operators. |
| Seasonality | int | Controls the seasonal analysis. The possible values are: - -1: Autodetect seasonality using series_periods_detect. This is the default value.- Period: A positive integer specifying the expected period in number of bins. For example, if the series is in 1 - h bins, a weekly period is 168 bins.- 0: No seasonality, so skip extracting this component. | |
| Trend | string | Controls the trend analysis. The possible values are: - avg: Define trend component as average(x). This is the default.- linefit: Extract trend component using linear regression.- none: No trend, so skip extracting this component. | |
| Test_points | int | A positive integer specifying the number of points at the end of the series to exclude from the learning, or regression, process. This parameter should be set for forecasting purposes. The default value is 0. | |
| Seasonality_threshold | real | The threshold for seasonality score when Seasonality is set to autodetect. The default score threshold is 0.6. For more information, see series_periods_detect. |
Returns
The function returns the following respective series:
baseline: the predicted value of the series (sum of seasonal and trend components, see below).seasonal: the series of the seasonal component:- if the period isn’t detected or is explicitly set to 0: constant 0.
- if detected or set to positive integer: median of the series points in the same phase
trend: the series of the trend component.residual: the series of the residual component (that is, x - baseline).
More about series decomposition
This method is usually applied to time series of metrics expected to manifest periodic and/or trend behavior. You can use the method to forecast future metric values and/or detect anomalous values. The implicit assumption of this regression process is that apart from seasonal and trend behavior, the time series is stochastic and randomly distributed. Forecast future metric values from the seasonal and trend components while ignoring the residual part. Detect anomalous values based on outlier detection only on the residual part only. Further details can be found in the Time Series Decomposition chapter.
Examples
Weekly seasonality
In the following example, we generate a series with weekly seasonality and without trend, we then add some outliers to it. series_decompose finds and automatically detects the seasonality, and generates a baseline that is almost identical to the seasonal component. The outliers we added can be clearly seen in the residuals component.
let ts=range t from 1 to 24*7*5 step 1
| extend Timestamp = datetime(2018-03-01 05:00) + 1h * t
| extend y = 2*rand() + iff((t/24)%7>=5, 10.0, 15.0) - (((t%24)/10)*((t%24)/10)) // generate a series with weekly seasonality
| extend y=iff(t==150 or t==200 or t==780, y-8.0, y) // add some dip outliers
| extend y=iff(t==300 or t==400 or t==600, y+8.0, y) // add some spike outliers
| summarize Timestamp=make_list(Timestamp, 10000),y=make_list(y, 10000);
ts
| extend series_decompose(y)
| render timechart
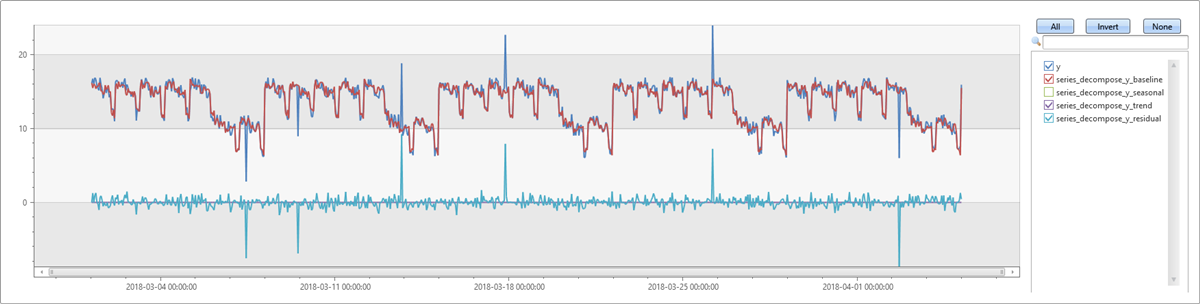
Weekly seasonality with trend
In this example, we add a trend to the series from the previous example. First, we run series_decompose with the default parameters. The trend avg default value only takes the average and doesn’t compute the trend. The generated baseline doesn’t contain the trend. When observing the trend in the residuals, it becomes apparent that this example is less accurate than the previous example.
let ts=range t from 1 to 24*7*5 step 1
| extend Timestamp = datetime(2018-03-01 05:00) + 1h * t
| extend y = 2*rand() + iff((t/24)%7>=5, 5.0, 15.0) - (((t%24)/10)*((t%24)/10)) + t/72.0 // generate a series with weekly seasonality and ongoing trend
| extend y=iff(t==150 or t==200 or t==780, y-8.0, y) // add some dip outliers
| extend y=iff(t==300 or t==400 or t==600, y+8.0, y) // add some spike outliers
| summarize Timestamp=make_list(Timestamp, 10000),y=make_list(y, 10000);
ts
| extend series_decompose(y)
| render timechart
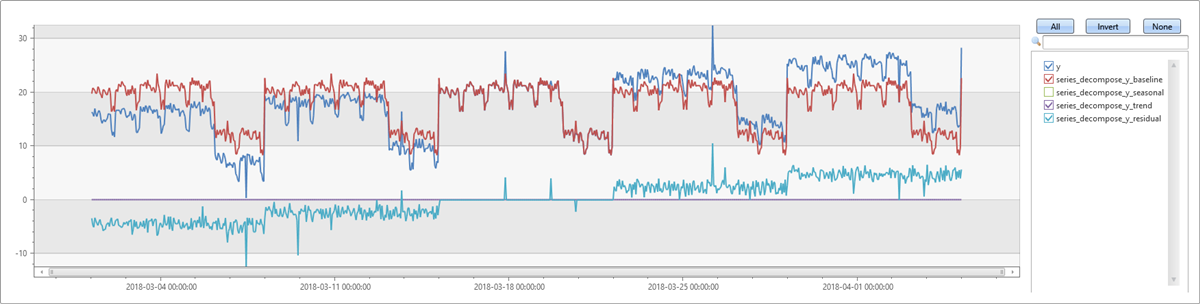
Next, we rerun the same example. Since we’re expecting a trend in the series, we specify linefit in the trend parameter. We can see that the positive trend is detected and the baseline is much closer to the input series. The residuals are close to zero, and only the outliers stand out. We can see all the components on the series in the chart.
let ts=range t from 1 to 24*7*5 step 1
| extend Timestamp = datetime(2018-03-01 05:00) + 1h * t
| extend y = 2*rand() + iff((t/24)%7>=5, 5.0, 15.0) - (((t%24)/10)*((t%24)/10)) + t/72.0 // generate a series with weekly seasonality and ongoing trend
| extend y=iff(t==150 or t==200 or t==780, y-8.0, y) // add some dip outliers
| extend y=iff(t==300 or t==400 or t==600, y+8.0, y) // add some spike outliers
| summarize Timestamp=make_list(Timestamp, 10000),y=make_list(y, 10000);
ts
| extend series_decompose(y, -1, 'linefit')
| render timechart
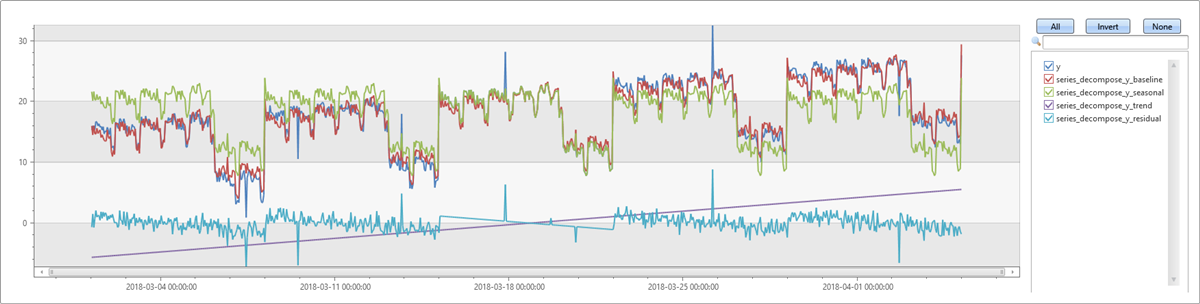
Related content
- Visualize results with an anomalychart
13 - series_divide()
Calculates the element-wise division of two numeric series inputs.
Syntax
series_divide(series1, series2)
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| series1, series2 | dynamic | ✔️ | The numeric arrays over which to calculate the element-wise division. The first array is to be divided by the second. |
Returns
Dynamic array of calculated element-wise divide operation between the two inputs. Any non-numeric element or non-existing element (arrays of different sizes) yields a null element value.
Note: the result series is of double type, even if the inputs are integers. Division by zero follows the double division by zero (e.g. 2/0 yields double(+inf)).
Example
range x from 1 to 3 step 1
| extend y = x * 2
| extend z = y * 2
| project s1 = pack_array(x,y,z), s2 = pack_array(z, y, x)
| extend s1_divide_s2 = series_divide(s1, s2)
Output
| s1 | s2 | s1_divide_s2 |
|---|---|---|
| [1,2,4] | [4,2,1] | [0.25,1.0,4.0] |
| [2,4,8] | [8,4,2] | [0.25,1.0,4.0] |
| [3,6,12] | [12,6,3] | [0.25,1.0,4.0] |
14 - series_dot_product()
Calculates the dot product of two numeric series.
The function series_dot_product() takes two numeric series as input, and calculates their dot product.
Syntax
series_dot_product(series1, series2)
Alternate syntax
series_dot_product(series, numeric)
series_dot_product(numeric, series)
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| series1, series2 | dynamic | ✔️ | Input arrays with numeric data, to be element-wise multiplied and then summed into a value of type real. |
Returns
Returns a value of type real whose value is the sum over the product of each element of series1 with the corresponding element of series2.
In case both series length isn’t equal, the longer series will be truncated to the length of the shorter one.
Any non-numeric element of the input series will be ignored.
Example
range x from 1 to 3 step 1
| extend y = x * 2
| extend z = y * 2
| project s1 = pack_array(x,y,z), s2 = pack_array(z, y, x)
| extend s1_dot_product_s2 = series_dot_product(s1, s2)
| s1 | s2 | s1_dot_product_s2 |
|---|---|---|
| [1,2,4] | [4,2,1] | 12 |
| [2,4,8] | [8,4,2] | 48 |
| [3,6,12] | [12,6,3] | 108 |
range x from 1 to 3 step 1
| extend y = x * 2
| extend z = y * 2
| project s1 = pack_array(x,y,z), s2 = x
| extend s1_dot_product_s2 = series_dot_product(s1, s2)
| s1 | s2 | s1_dot_product_s2 |
|---|---|---|
| [1,2,4] | 1 | 7 |
| [2,4,8] | 2 | 28 |
| [3,6,12] | 3 | 63 |
15 - series_equals()
==) logic operation of two numeric series inputs.Calculates the element-wise equals (==) logic operation of two numeric series inputs.
Syntax
series_equals (series1, series2)
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| series1, series2 | dynamic | ✔️ | The numeric arrays to be element-wise compared. |
Returns
Dynamic array of booleans containing the calculated element-wise equal logic operation between the two inputs. Any non-numeric element or non-existing element (arrays of different sizes) yields a null element value.
Example
print s1 = dynamic([1,2,4]), s2 = dynamic([4,2,1])
| extend s1_equals_s2 = series_equals(s1, s2)
Output
| s1 | s2 | s1_equals_s2 |
|---|---|---|
| [1,2,4] | [4,2,1] | [false,true,false] |
Related content
For entire series statistics comparisons, see:
16 - series_exp()
Calculates the element-wise base-e exponential function (e^x) of the numeric series input.
Syntax
series_exp(series)
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| series | dynamic | ✔️ | An array of numeric values whose elements are applied as the exponent in the exponential function. |
Returns
Dynamic array of calculated exponential function. Any non-numeric element yields a null element value.
Example
print s = dynamic([1,2,3])
| extend s_exp = series_exp(s)
Output
| s | s_exp |
|---|---|
| [1,2,3] | [2.7182818284590451,7.38905609893065,20.085536923187668] |
17 - series_fft()
Applies the Fast Fourier Transform (FFT) on a series.
The series_fft() function takes a series of complex numbers in the time/spatial domain and transforms it to the frequency domain using the Fast Fourier Transform. The transformed complex series represents the magnitude and phase of the frequencies appearing in the original series. Use the complementary function series_ifft to transform from the frequency domain back to the time/spatial domain.
Syntax
series_fft(x_real [, x_imaginary])
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| x_real | dynamic | ✔️ | A numeric array representing the real component of the series to transform. |
| x_imaginary | dynamic | A similar array representing the imaginary component of the series. This parameter should only be specified if the input series contains complex numbers. |
Returns
The function returns the complex inverse fft in two series. The first series for the real component and the second one for the imaginary component.
Example
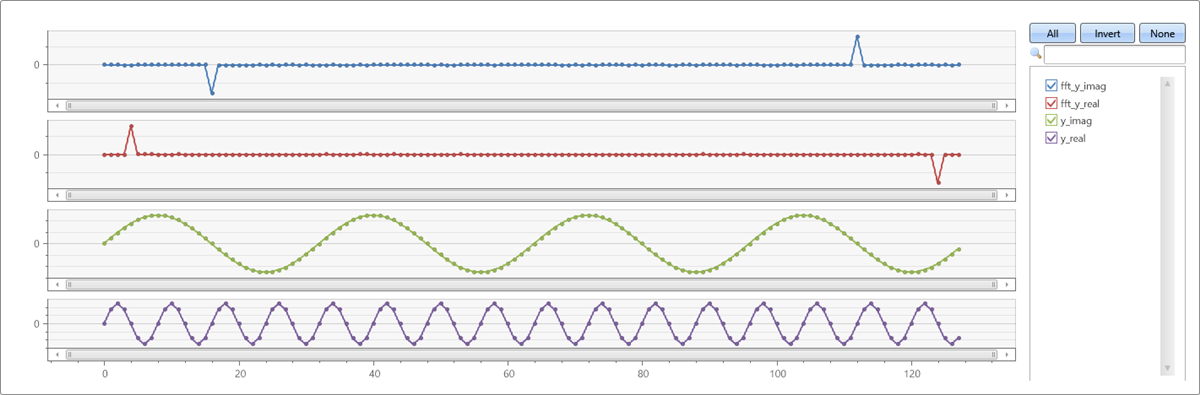
Generate a complex series, where the real and imaginary components are pure sine waves in different frequencies. Use FFT to transform it to the frequency domain:
[!div class=“nextstepaction”] Run the query
let sinewave=(x:double, period:double, gain:double=1.0, phase:double=0.0) { gain*sin(2*pi()/period*(x+phase)) } ; let n=128; // signal length range x from 0 to n-1 step 1 | extend yr=sinewave(x, 8), yi=sinewave(x, 32) | summarize x=make_list(x), y_real=make_list(yr), y_imag=make_list(yi) | extend (fft_y_real, fft_y_imag) = series_fft(y_real, y_imag) | render linechart with(ysplit=panels)This query returns fft_y_real and fft_y_imag:
Transform a series to the frequency domain, and then apply the inverse transform to get back the original series:
[!div class=“nextstepaction”] Run the query
let sinewave=(x:double, period:double, gain:double=1.0, phase:double=0.0) { gain*sin(2*pi()/period*(x+phase)) } ; let n=128; // signal length range x from 0 to n-1 step 1 | extend yr=sinewave(x, 8), yi=sinewave(x, 32) | summarize x=make_list(x), y_real=make_list(yr), y_imag=make_list(yi) | extend (fft_y_real, fft_y_imag) = series_fft(y_real, y_imag) | extend (y_real2, y_image2) = series_ifft(fft_y_real, fft_y_imag) | project-away fft_y_real, fft_y_imag // too many series for linechart with panels | render linechart with(ysplit=panels)This query returns y_real2 and *y_imag2, which are the same as y_real and y_imag:
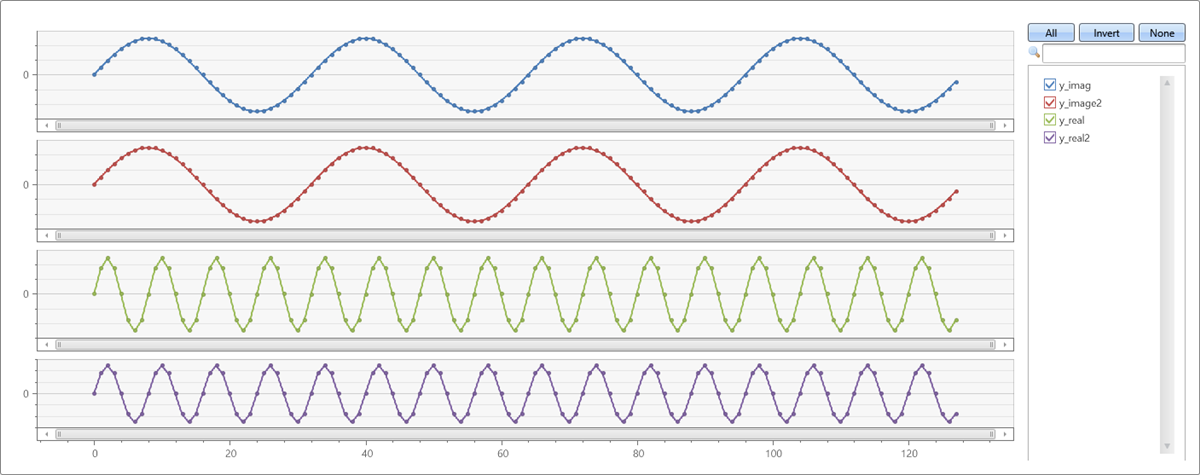
18 - series_fill_backward()
Performs a backward fill interpolation of missing values in a series.
An expression containing dynamic numerical array is the input. The function replaces all instances of missing_value_placeholder with the nearest value from its right side (other than missing_value_placeholder), and returns the resulting array. The rightmost instances of missing_value_placeholder are preserved.
Syntax
series_fill_backward(series[,missing_value_placeholder])
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| series | dynamic | ✔️ | An array of numeric values. |
| missing_value_placeholder | scalar | Specifies a placeholder for missing values. The default value is double(null). The value can be of any type that converts to actual element types. double(null), long(null), and int(null) have the same meaning. |
Returns
series with all instances of missing_value_placeholder filled backwards.
Example
The following example performs a backwards fill on missing data in the datatable, data.
let data = datatable(arr: dynamic)
[
dynamic([111, null, 36, 41, null, null, 16, 61, 33, null, null])
];
data
| project
arr,
fill_backward = series_fill_backward(arr)
Output
arr | fill_backward |
|---|---|
| [111,null,36,41,null,null,16,61,33,null,null] | [111,36,36,41,16,16,16,61,33,null,null] |
Related content
19 - series_fill_const()
Replaces missing values in a series with a specified constant value.
Takes an expression containing dynamic numerical array as input, replaces all instances of missing_value_placeholder with the specified constant_value and returns the resulting array.
Syntax
series_fill_const(series, constant_value, [ missing_value_placeholder ])
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| series | dynamic | ✔️ | An array of numeric values. |
| constant_value | scalar | ✔️ | The value used to replace the missing values. |
| missing_value_placeholder | scalar | Specifies a placeholder for missing values. The default value is double(null). The value can be of any type that is converted to actual element types. double(null), long(null), and int(null) have the same meaning. |
Returns
series with all instances of missing_value_placeholder replaced with constant_value.
Example
The following example replaces the missing values in the datatable, data, with the value 0.0 in column fill_const1 and with the value -1 in column fill_const2.
let data = datatable(arr: dynamic)
[
dynamic([111, null, 36, 41, 23, null, 16, 61, 33, null, null])
];
data
| project
arr,
fill_const1 = series_fill_const(arr, 0.0),
fill_const2 = series_fill_const(arr, -1)
Output
arr | fill_const1 | fill_const2 |
|---|---|---|
| [111,null,36,41,23,null,16,61,33,null,null] | [111,0.0,36,41,23,0.0,16,61,33,0.0,0.0] | [111,-1,36,41,23,-1,16,61,33,-1,-1] |
Related content
20 - series_fill_forward()
Performs a forward fill interpolation of missing values in a series.
An expression containing dynamic numerical array is the input. The function replaces all instances of missing_value_placeholder with the nearest value from its left side other than missing_value_placeholder, and returns the resulting array. The leftmost instances of missing_value_placeholder are preserved.
Syntax
series_fill_forward(series, [ missing_value_placeholder ])
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| series | dynamic | ✔️ | An array of numeric values. |
| missing_value_placeholder | scalar | Specifies a placeholder for missing values. The default value is double(null). The value can be of any type that can convert to actual element types. double(null), long(null), and int(null) have the same meaning. |
Returns
series with all instances of missing_value_placeholder filled forwards.
Example
The following example performs a forward fill on missing data in the datatable, data.
let data = datatable(arr: dynamic)
[
dynamic([null, null, 36, 41, null, null, 16, 61, 33, null, null])
];
data
| project
arr,
fill_forward = series_fill_forward(arr)
Output
arr | fill_forward |
|---|---|
| [null,null,36,41,null,null,16,61,33,null,null] | [null,null,36,41,41,41,16,61,33,33,33] |
Use series_fill_backward or series-fill-const to complete interpolation of the array.
Related content
21 - series_fill_linear()
Linearly interpolates missing values in a series.
Takes an expression containing dynamic numerical array as input, does linear interpolation for all instances of missing_value_placeholder, and returns the resulting array. If the beginning and end of the array contain missing_value_placeholder, then it’s replaced with the nearest value other than missing_value_placeholder. This feature can be turned off. If the whole array consists of the missing_value_placeholder, the array is filled with constant_value, or 0 if not specified.
Syntax
series_fill_linear(series, [ missing_value_placeholder [,fill_edges [, constant_value ]]])
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| series | dynamic | ✔️ | An array of numeric values. |
| missing_value_placeholder | scalar | Specifies a placeholder for missing values. The default value is double(null). The value can be of any type that can convert to actual element types. double(null), long(null), and int(null) have the same meaning. | |
| fill_edges | bool | Indicates whether missing_value_placeholder at the start and end of the array should be replaced with nearest value. true by default. If set to false, then missing_value_placeholder at the start and end of the array is preserved. | |
| constant_value | scalar | Relevant only for arrays that entirely consist of null values. This parameter specifies a constant value with which to fill the series. Default value is 0. Setting this parameter it to double(null) preserves the null values. |
Returns
A series linear interpolation of series using the specified parameters. If series contains only int or long elements, then the linear interpolation returns rounded interpolated values rather than exact ones.
Example
The following example shows how to use use the series_fill_linear() function to fill missing values (nulls) in the arrays using linear interpolation. It fills values using the original arr without additional arguments, using edge values, and excluding edge values.
let data = datatable(arr: dynamic)
[
dynamic([null, 111.0, null, 36.0, 41.0, null, null, 16.0, 61.0, 33.0, null, null]), // Array of double
dynamic([null, 111, null, 36, 41, null, null, 16, 61, 33, null, null]), // Similar array of int
dynamic([null, null, null, null]) // Array with missing values only
];
data
| project
arr,
without_args = series_fill_linear(arr),
with_edges = series_fill_linear(arr, double(null), true),
wo_edges = series_fill_linear(arr, double(null), false),
with_const = series_fill_linear(arr, double(null), true, 3.14159)
Output
arr | without_args | with_edges | wo_edges | with_const |
|---|---|---|---|---|
| [null,111.0,null,36.0,41.0,null,null,16.0,61.0,33.0,null,null] | [111.0,111.0,73.5,36.0,41.0,32.667,24.333,16.0,61.0,33.0,33.0,33.0] | [111.0,111.0,73.5,36.0,41.0,32.667,24.333,16.0,61.0,33.0,33.0,33.0] | [null,111.0,73.5,36.0,41.0,32.667,24.333,16.0,61.0,33.0,null,null] | [111.0,111.0,73.5,36.0,41.0,32.667,24.333,16.0,61.0,33.0,33.0,33.0] |
| [null,111,null,36,41,null,null,16,61,33,null,null] | [111,111,73,36,41,32,24,16,61,33,33,33] | [111,111,73,36,41,32,24,16,61,33,33,33] | [null,111,73,36,41,32,24,16,61,33,null,null] | [111,111,74,38, 41,32,24,16,61,33,33,33] |
| [null,null,null,null] | [0.0,0.0,0.0,0.0] | [0.0,0.0,0.0,0.0] | [0.0,0.0,0.0,0.0] | [3.14159,3.14159,3.14159,3.14159] |
Related content
22 - series_fir()
Applies a Finite Impulse Response (FIR) filter on a series.
The function takes an expression containing a dynamic numerical array as input and applies a Finite Impulse Response filter. By specifying the filter coefficients, it can be used for calculating a moving average, smoothing, change-detection, and many more use cases. The function takes the column containing the dynamic array and a static dynamic array of the filter’s coefficients as input, and applies the filter on the column. It outputs a new dynamic array column, containing the filtered output.
Syntax
series_fir(series, filter [, normalize[, center]])
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| series | dynamic | ✔️ | An array of numeric values. |
| filter | dynamic | ✔️ | An array of numeric values containing the coefficients of the filter. |
| normalize | bool | Indicates whether the filter should be normalized. That is, divided by the sum of the coefficients. If filter contains negative values, then normalize must be specified as false, otherwise result will be null. If not specified, then a default value of true is assumed, depending on the presence of negative values in the filter. If filter contains at least one negative value, then normalize is assumed to be false. | |
| center | bool | Indicates whether the filter is applied symmetrically on a time window before and after the current point, or on a time window from the current point backwards. By default, center is false, which fits the scenario of streaming data so that we can only apply the filter on the current and older points. However, for ad-hoc processing you can set it to true, keeping it synchronized with the time series. See examples below. This parameter controls the filter’s group delay. |
Returns
A new dynamic array column containing the filtered output.
Examples
- Calculate a moving average of five points by setting filter=[1,1,1,1,1] and normalize=
true(default). Note the effect of center=false(default) vs.true:
range t from bin(now(), 1h) - 23h to bin(now(), 1h) step 1h
| summarize t=make_list(t)
| project
id='TS',
val=dynamic([0, 0, 0, 0, 0, 0, 0, 0, 0, 10, 20, 40, 100, 40, 20, 10, 0, 0, 0, 0, 0, 0, 0, 0]),
t
| extend
5h_MovingAvg=series_fir(val, dynamic([1, 1, 1, 1, 1])),
5h_MovingAvg_centered=series_fir(val, dynamic([1, 1, 1, 1, 1]), true, true)
| render timechart
This query returns:
5h_MovingAvg: Five points moving average filter. The spike is smoothed and its peak shifted by (5-1)/2 = 2h.
5h_MovingAvg_centered: Same, but by setting center=true, the peak stays in its original location.
- To calculate the difference between a point and its preceding one, set filter=[1,-1].
range t from bin(now(), 1h) - 11h to bin(now(), 1h) step 1h
| summarize t=make_list(t)
| project id='TS', t, value=dynamic([0, 0, 0, 0, 2, 2, 2, 2, 3, 3, 3, 3])
| extend diff=series_fir(value, dynamic([1, -1]), false, false)
| render timechart
23 - series_fit_2lines_dynamic()
Applies two segments linear regression on a series, returning a dynamic object.
Takes an expression containing dynamic numerical array as input and applies two segments linear regression in order to identify and quantify trend changes in a series. The function iterates on the series indexes. In each iteration, it splits the series to two parts, and fits a separate line using series_fit_line() or series_fit_line_dynamic(). The function fits the lines to each of the two parts, and calculates the total R-squared value. The best split is the one that maximizes R-squared. The function returns its parameters in dynamic value with the following content:
rsquare: R-squared is a standard measure of the fit quality. It’s a number in the range of [0-1], where 1 is the best possible fit, and 0 means the data is unordered and don’t fit any line.split_idx: the index of breaking point to two segments (zero-based).variance: variance of the input data.rvariance: residual variance that is the variance between the input data values the approximated ones (by the two line segments).line_fit: numerical array holding a series of values of the best fitted line. The series length is equal to the length of the input array. It’s used for charting.right.rsquare: r-square of the line on the right side of the split, see series_fit_line() or series_fit_line_dynamic().right.slope: slope of the right approximated line (of the form y=ax+b).right.interception: interception of the approximated left line (b from y=ax+b).right.variance: variance of the input data on the right side of the split.right.rvariance: residual variance of the input data on the right side of the split.left.rsquare: r-square of the line on the left side of the split, see [series_fit_line()].(series-fit-line-function.md) or series_fit_line_dynamic().left.slope: slope of the left approximated line (of the form y=ax+b).left.interception: interception of the approximated left line (of the form y=ax+b).left.variance: variance of the input data on the left side of the split.left.rvariance: residual variance of the input data on the left side of the split.
This operator is similar to series_fit_2lines. Unlike series-fit-2lines, it returns a dynamic bag.
Syntax
series_fit_2lines_dynamic(series)
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| series | dynamic | ✔️ | An array of numeric values. |
Example
print
id=' ',
x=range(bin(now(), 1h) - 11h, bin(now(), 1h), 1h),
y=dynamic([1, 2.2, 2.5, 4.7, 5.0, 12, 10.3, 10.3, 9, 8.3, 6.2])
| extend
LineFit=series_fit_line_dynamic(y).line_fit,
LineFit2=series_fit_2lines_dynamic(y).line_fit
| project id, x, y, LineFit, LineFit2
| render timechart
24 - series_fit_2lines()
Applies a two segmented linear regression on a series, returning multiple columns.
Takes an expression containing dynamic numerical array as input and applies a two segmented linear regression in order to identify and quantify a trend change in a series. The function iterates on the series indexes. In each iteration, the function splits the series to two parts, fits a separate line (using series_fit_line()) to each part, and calculates the total r-square. The best split is the one that maximized r-square; the function returns its parameters:
| Parameter | Description |
|---|---|
rsquare | R-square is standard measure of the fit quality. It’s a number in the range [0-1], where 1 - is the best possible fit, and 0 means the data is unordered and don’t fit any line. |
split_idx | The index of breaking point to two segments (zero-based). |
variance | Variance of the input data. |
rvariance | Residual variance, which is the variance between the input data values the approximated ones (by the two line segments). |
line_fit | Numerical array holding a series of values of the best fitted line. The series length is equal to the length of the input array. It’s mainly used for charting. |
right_rsquare | R-square of the line on the right side of the split, see series_fit_line(). |
right_slope | Slope of the right approximated line (of the form y=ax+b). |
right_interception | Interception of the approximated left line (b from y=ax+b). |
right_variance | Variance of the input data on the right side of the split. |
right_rvariance | Residual variance of the input data on the right side of the split. |
left_rsquare | R-square of the line on the left side of the split, see series_fit_line(). |
left_slope | Slope of the left approximated line (of the form y=ax+b). |
left_interception | Interception of the approximated left line (of the form y=ax+b). |
left_variance | Variance of the input data on the left side of the split. |
left_rvariance | Residual variance of the input data on the left side of the split. |
Syntax
project series_fit_2lines(series)
- Will return all mentioned above columns with the following names: series_fit_2lines_x_rsquare, series_fit_2lines_x_split_idx etc.
project (rs, si, v)=series_fit_2lines(series)
- Will return the following columns: rs (r-square), si (split index), v (variance) and the rest will look like series_fit_2lines_x_rvariance, series_fit_2lines_x_line_fit and etc.
extend (rs, si, v)=series_fit_2lines(series)
- Will return only: rs (r-square), si (split index) and v (variance).
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| series | dynamic | ✔️ | An array of numeric values. |
Examples
print
id=' ',
x=range(bin(now(), 1h) - 11h, bin(now(), 1h), 1h),
y=dynamic([1, 2.2, 2.5, 4.7, 5.0, 12, 10.3, 10.3, 9, 8.3, 6.2])
| extend
(Slope, Interception, RSquare, Variance, RVariance, LineFit)=series_fit_line(y),
(RSquare2, SplitIdx, Variance2, RVariance2, LineFit2)=series_fit_2lines(y)
| project id, x, y, LineFit, LineFit2
| render timechart

25 - series_fit_line_dynamic()
Applies linear regression on a series, returning dynamic object.
Takes an expression containing dynamic numerical array as input, and does linear regression to find the line that best fits it. This function should be used on time series arrays, fitting the output of make-series operator. It generates a dynamic value with the following content:
rsquare: r-square is a standard measure of the fit quality. It’s a number in the range [0-1], where 1 is the best possible fit, and 0 means the data is unordered and doesn’t fit any lineslope: Slope of the approximated line (the a-value from y=ax+b)variance: Variance of the input datarvariance: Residual variance that is the variance between the input data values and the approximated ones.interception: Interception of the approximated line (the b-value from y=ax+b)line_fit: Numerical array containing a series of values of the best fit line. The series length is equal to the length of the input array. It’s used mainly for charting.
This operator is similar to series_fit_line, but unlike series-fit-line it returns a dynamic bag.
Syntax
series_fit_line_dynamic(series)
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| series | dynamic | ✔️ | An array of numeric values. |
Examples
print
id=' ',
x=range(bin(now(), 1h) - 11h, bin(now(), 1h), 1h),
y=dynamic([2, 5, 6, 8, 11, 15, 17, 18, 25, 26, 30, 30])
| extend fit=series_fit_line_dynamic(y)
| extend
RSquare=fit.rsquare,
Slope=fit.slope,
Variance=fit.variance,
RVariance=fit.rvariance,
Interception=fit.interception,
LineFit=fit.line_fit
| render timechart
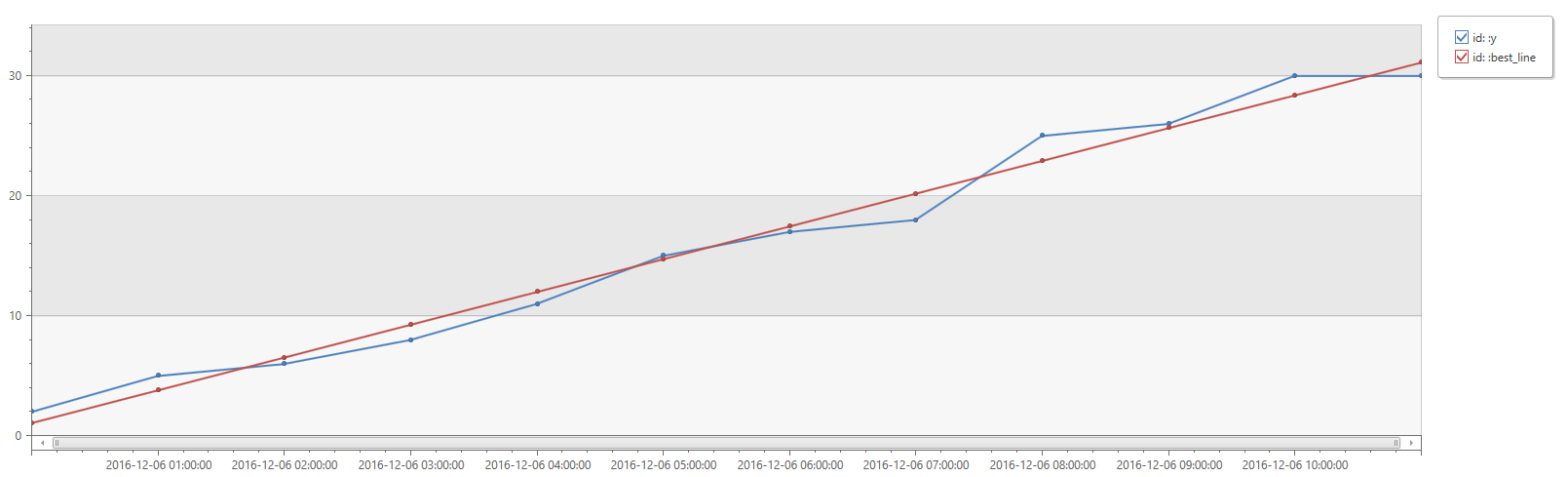
| RSquare | Slope | Variance | RVariance | Interception | LineFit |
|---|---|---|---|---|---|
| 0.982 | 2.730 | 98.628 | 1.686 | -1.666 | 1.064, 3.7945, 6.526, 9.256, 11.987, 14.718, 17.449, 20.180, 22.910, 25.641, 28.371, 31.102 |
26 - series_fit_line()
Applies linear regression on a series, returning multiple columns.
Takes an expression containing dynamic numerical array as input and does linear regression to find the line that best fits it. This function should be used on time series arrays, fitting the output of make-series operator. The function generates the following columns:
rsquare: r-square is a standard measure of the fit quality. The value’s a number in the range [0-1], where 1 - is the best possible fit, and 0 means the data is unordered and doesn’t fit any line.slope: Slope of the approximated line (“a” from y=ax+b).variance: Variance of the input data.rvariance: Residual variance that is the variance between the input data values the approximated ones.interception: Interception of the approximated line (“b” from y=ax+b).line_fit: Numerical array holding a series of values of the best fitted line. The series length is equal to the length of the input array. The value’s used for charting.
Syntax
series_fit_line(series)
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| series | dynamic | ✔️ | An array of numeric values. |
Examples
print
id=' ',
x=range(bin(now(), 1h) - 11h, bin(now(), 1h), 1h),
y=dynamic([2, 5, 6, 8, 11, 15, 17, 18, 25, 26, 30, 30])
| extend (RSquare, Slope, Variance, RVariance, Interception, LineFit)=series_fit_line(y)
| render timechart

| RSquare | Slope | Variance | RVariance | Interception | LineFit |
|---|---|---|---|---|---|
| 0.982 | 2.730 | 98.628 | 1.686 | -1.666 | 1.064, 3.7945, 6.526, 9.256, 11.987, 14.718, 17.449, 20.180, 22.910, 25.641, 28.371, 31.102 |
27 - series_fit_poly()
Applies a polynomial regression from an independent variable (x_series) to a dependent variable (y_series). This function takes a table containing multiple series (dynamic numerical arrays) and generates the best fit high-order polynomial for each series using polynomial regression.
Syntax
T | extend series_fit_poly(y_series [, x_series, degree ])
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| y_series | dynamic | ✔️ | An array of numeric values containing the dependent variable. |
| x_series | dynamic | An array of numeric values containing the independent variable. Required only for unevenly spaced series. If not specified, it’s set to a default value of [1, 2, …, length(y_series)]. | |
| degree | The required order of the polynomial to fit. For example, 1 for linear regression, 2 for quadratic regression, and so on. Defaults to 1, which indicates linear regression. |
Returns
The series_fit_poly() function returns the following columns:
rsquare: r-square is a standard measure of the fit quality. The value’s a number in the range [0-1], where 1 - is the best possible fit, and 0 means the data is unordered and doesn’t fit any line.coefficients: Numerical array holding the coefficients of the best fitted polynomial with the given degree, ordered from the highest power coefficient to the lowest.variance: Variance of the dependent variable (y_series).rvariance: Residual variance that is the variance between the input data values the approximated ones.poly_fit: Numerical array holding a series of values of the best fitted polynomial. The series length is equal to the length of the dependent variable (y_series). The value’s used for charting.
Examples
Example 1
A fifth order polynomial with noise on x & y axes:
range x from 1 to 200 step 1
| project x = rand()*5 - 2.3
| extend y = pow(x, 5)-8*pow(x, 3)+10*x+6
| extend y = y + (rand() - 0.5)*0.5*y
| summarize x=make_list(x), y=make_list(y)
| extend series_fit_poly(y, x, 5)
| project-rename fy=series_fit_poly_y_poly_fit, coeff=series_fit_poly_y_coefficients
|fork (project x, y, fy) (project-away x, y, fy)
| render linechart
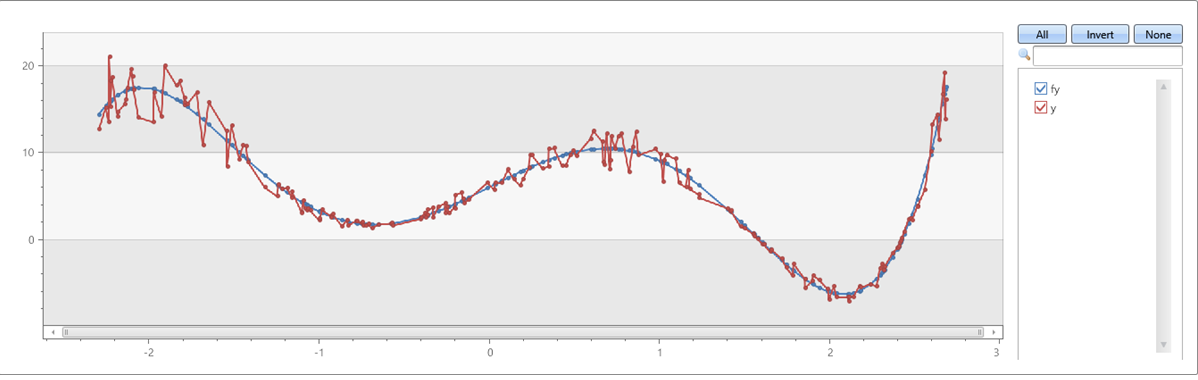
Example 2
Verify that series_fit_poly with degree=1 matches series_fit_line:
demo_series1
| extend series_fit_line(y)
| extend series_fit_poly(y)
| project-rename y_line = series_fit_line_y_line_fit, y_poly = series_fit_poly_y_poly_fit
| fork (project x, y, y_line, y_poly) (project-away id, x, y, y_line, y_poly)
| render linechart with(xcolumn=x, ycolumns=y, y_line, y_poly)
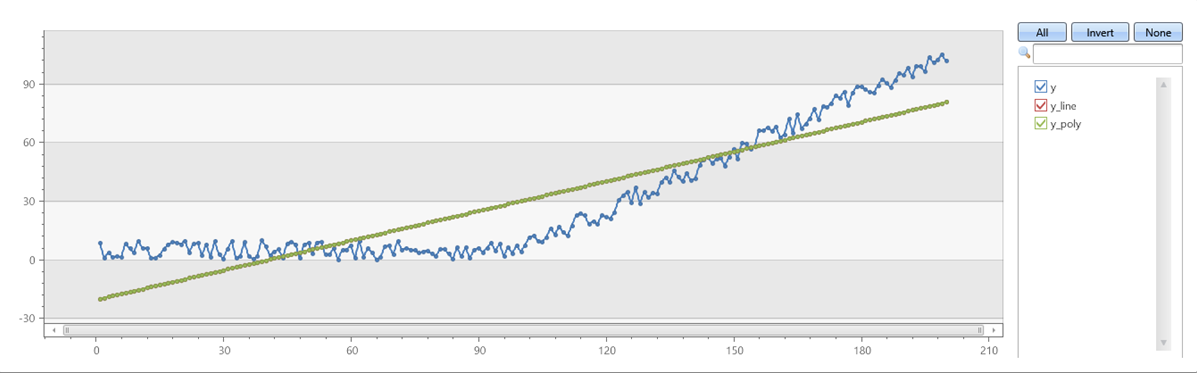

Example 3
Irregular (unevenly spaced) time series:
//
// x-axis must be normalized to the range [0-1] if either degree is relatively big (>= 5) or original x range is big.
// so if x is a time axis it must be normalized as conversion of timestamp to long generate huge numbers (number of 100 nano-sec ticks from 1/1/1970)
//
// Normalization: x_norm = (x - min(x))/(max(x) - min(x))
//
irregular_ts
| extend series_stats(series_add(TimeStamp, 0)) // extract min/max of time axis as doubles
| extend x = series_divide(series_subtract(TimeStamp, series_stats__min), series_stats__max-series_stats__min) // normalize time axis to [0-1] range
| extend series_fit_poly(num, x, 8)
| project-rename fnum=series_fit_poly_num_poly_fit
| render timechart with(ycolumns=num, fnum)
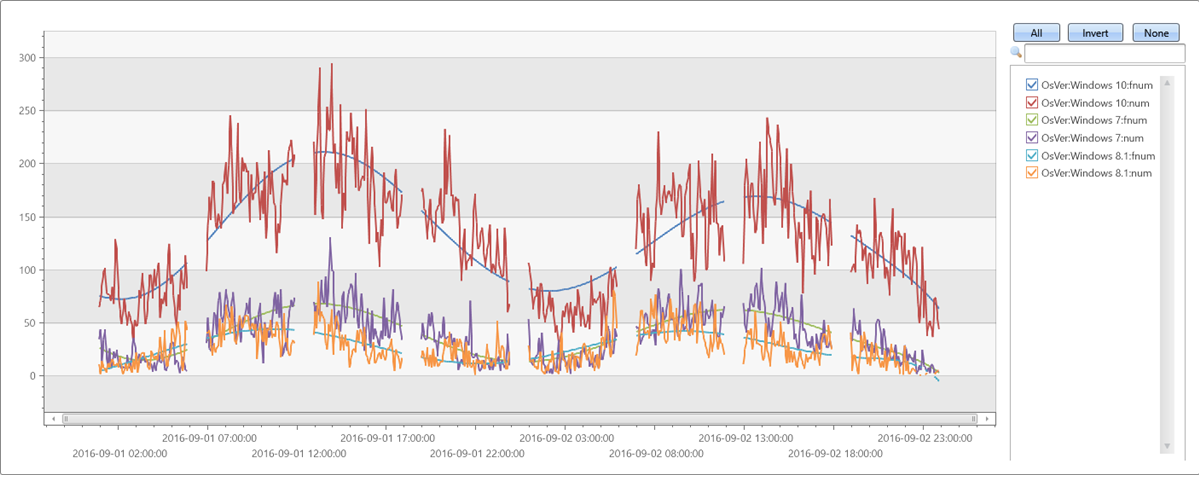
28 - series_floor()
Calculates the element-wise floor function of the numeric series input.
Syntax
series_floor(series)
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| series | dynamic | ✔️ | An array of numeric values on which the floor function is applied. |
Returns
Dynamic array of the calculated floor function. Any non-numeric element yields a null element value.
Example
print s = dynamic([-1.5,1,2.5])
| extend s_floor = series_floor(s)
Output
| s | s_floor |
|---|---|
| [-1.5,1,2.5] | [-2.0,1.0,2.0] |
29 - series_greater_equals()
>=) logic operation of two numeric series inputs.Calculates the element-wise greater or equals (>=) logic operation of two numeric series inputs.
Syntax
series_greater_equals(series1, series2)
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| series1, series2 | dynamic | ✔️ | The arrays of numeric values to be element-wise compared. |
Returns
Dynamic array of booleans containing the calculated element-wise greater or equal logic operation between the two inputs. Any non-numeric element or non-existing element (arrays of different sizes) yields a null element value.
Example
print s1 = dynamic([1,2,4]), s2 = dynamic([4,2,1])
| extend s1_greater_equals_s2 = series_greater_equals(s1, s2)
Output
| s1 | s2 | s1_greater_equals_s2 |
|---|---|---|
| [1,2,4] | [4,2,1] | [false,true,true] |
Related content
For entire series statistics comparisons, see:
30 - series_greater()
>) logic operation of two numeric series inputs.Calculates the element-wise greater (>) logic operation of two numeric series inputs.
Syntax
series_greater(series1, series2)
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| series1, series2 | dynamic | ✔️ | The arrays of numeric values to be element-wise compared. |
Returns
Dynamic array of booleans containing the calculated element-wise greater logic operation between the two inputs. Any non-numeric element or non-existing element (arrays of different sizes) yields a null element value.
Example
print s1 = dynamic([1,2,4]), s2 = dynamic([4,2,1])
| extend s1_greater_s2 = series_greater(s1, s2)
Output
| s1 | s2 | s1_greater_s2 |
|---|---|---|
| [1,2,4] | [4,2,1] | [false,false,true] |
Related content
For entire series statistics comparisons, see:
31 - series_ifft()
Applies the Inverse Fast Fourier Transform (IFFT) on a series.
The series_ifft() function takes a series of complex numbers in the frequency domain and transforms it back to the time/spatial domain using the Fast Fourier Transform. This function is the complementary function of series_fft. Commonly the original series is transformed to the frequency domain for spectral processing and then back to the time/spatial domain.
Syntax
series_ifft(fft_real [, fft_imaginary])
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| fft_real | dynamic | ✔️ | An array of numeric values representing the real component of the series to transform. |
| fft_imaginary | dynamic | An array of numeric values representing the imaginary component of the series. This parameter should be specified only if the input series contains complex numbers. |
Returns
The function returns the complex inverse fft in two series. The first series for the real component and the second one for the imaginary component.
Example
See series_fft
32 - series_iir()
Applies an Infinite Impulse Response filter on a series.
The function takes an expression containing dynamic numerical array as input, and applies an Infinite Impulse Response filter. By specifying the filter coefficients, you can use the function to:
- calculate the cumulative sum of the series
- apply smoothing operations
- apply various high-pass, band-pass, and low-pass filters
The function takes as input the column containing the dynamic array and two static dynamic arrays of the filter’s denominators and numerators coefficients, and applies the filter on the column. It outputs a new dynamic array column, containing the filtered output.
Syntax
series_iir(series, numerators , denominators)
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| series | dynamic | ✔️ | An array of numeric values, typically the resulting output of make-series or make_list operators. |
| numerators | dynamic | ✔️ | An array of numeric values, containing the numerator coefficients of the filter. |
| denominators | dynamic | ✔️ | An array of numeric values, containing the denominator coefficients of the filter. |
The filter’s recursive formula
- Consider an input array X, and coefficients arrays a and b of lengths n_a and n_b respectively. The transfer function of the filter that will generate the output array Y, is defined by:
Example
Calculate a cumulative sum. Use the iir filter with coefficients denominators=[1,-1] and numerators=[1]:
let x = range(1.0, 10, 1);
print x=x, y = series_iir(x, dynamic([1]), dynamic([1,-1]))
| mv-expand x, y
Output
| x | y |
|---|---|
| 1.0 | 1.0 |
| 2.0 | 3.0 |
| 3.0 | 6.0 |
| 4.0 | 10.0 |
Here’s how to wrap it in a function:
let vector_sum=(x: dynamic) {
let y=array_length(x) - 1;
todouble(series_iir(x, dynamic([1]), dynamic([1, -1]))[y])
};
print d=dynamic([0, 1, 2, 3, 4])
| extend dd=vector_sum(d)
Output
| d | dd |
|---|---|
[0,1,2,3,4] | 10 |
33 - series_less_equals()
<=) logic operation of two numeric series inputs.Calculates the element-wise less or equal (<=) logic operation of two numeric series inputs.
Syntax
series_less_equals(series1, series2)
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| series1, series2 | dynamic | ✔️ | The arrays of numeric values to be element-wise compared. |
Returns
Dynamic array of booleans containing the calculated element-wise less or equal logic operation between the two inputs. Any non-numeric element or non-existing element (arrays of different sizes) yields a null element value.
Example
print s1 = dynamic([1,2,4]), s2 = dynamic([4,2,1])
| extend s1_less_equals_s2 = series_less_equals(s1, s2)
Output
| s1 | s2 | s1_less_equals_s2 |
|---|---|---|
| [1,2,4] | [4,2,1] | [true,true,false] |
Related content
For entire series statistics comparisons, see:
34 - series_less()
<) logic operation of two numeric series inputs.Calculates the element-wise less (<) logic operation of two numeric series inputs.
Syntax
series_less(series1, series2)
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| series1, series2 | dynamic | ✔️ | The arrays of numeric values to be element-wise compared. |
Returns
Dynamic array of booleans containing the calculated element-wise less logic operation between the two inputs. Any non-numeric element or non-existing element (arrays of different sizes) yields a null element value.
Example
print s1 = dynamic([1,2,4]), s2 = dynamic([4,2,1])
| extend s1_less_s2 = series_less(s1, s2)
Output
| s1 | s2 | s1_less_s2 |
|---|---|---|
| [1,2,4] | [4,2,1] | [true,false,false] |
Related content
For entire series statistics comparisons, see:
35 - series_log()
Calculates the element-wise natural logarithm function (base-e) of the numeric series input.
Syntax
series_log(series)
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| series | dynamic | ✔️ | An array of numeric values on which the natural logarithm function is applied. |
Returns
Dynamic array of the calculated natural logarithm function. Any non-numeric element yields a null element value.
Example
print s = dynamic([1,2,3])
| extend s_log = series_log(s)
Output
| s | s_log |
|---|---|
| [1,2,3] | [0.0,0.69314718055994529,1.0986122886681098] |
36 - series_magnitude()
Calculates the magnitude of series elements. This is equivalent to the square root of the dot product of the series with itself.
Syntax
series_magnitude(series)
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| series | dynamic | ✔️ | Array of numeric values. |
Returns
Returns a double type value representing the magnitude of the series.
Example
print arr=dynamic([1,2,3,4])
| extend series_magnitude=series_magnitude(arr)
Output
| s1 | s2 | series_magnitude |
|---|---|---|
| [1,2,3,4] | 5.4772255750516612 |
37 - series_multiply()
Calculates the element-wise multiplication of two numeric series inputs.
Syntax
series_multiply(series1, series2)
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| series1, series2 | dynamic | ✔️ | The arrays of numeric values to be element-wise multiplied. |
Returns
Dynamic array of calculated element-wise multiplication operation between the two inputs. Any non-numeric element or non-existing element (arrays of different sizes) yields a null element value.
Example
range x from 1 to 3 step 1
| extend y = x * 2
| extend z = y * 2
| project s1 = pack_array(x,y,z), s2 = pack_array(z, y, x)
| extend s1_multiply_s2 = series_multiply(s1, s2)
Output
| s1 | s2 | s1_multiply_s2 |
|---|---|---|
| [1,2,4] | [4,2,1] | [4,4,4] |
| [2,4,8] | [8,4,2] | [16,16,16] |
| [3,6,12] | [12,6,3] | [36,36,36] |
38 - series_not_equals()
!=) logic operation of two numeric series inputs.Calculates the element-wise not equals (!=) logic operation of two numeric series inputs.
Syntax
series_not_equals(series1, series2)
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| series1, series2 | dynamic | ✔️ | The arrays of numeric values to be element-wise compared. |
Returns
Dynamic array of booleans containing the calculated element-wise not equal logic operation between the two inputs. Any non-numeric element or non-existing element (arrays of different sizes) yields a null element value.
Example
print s1 = dynamic([1,2,4]), s2 = dynamic([4,2,1])
| extend s1_not_equals_s2 = series_not_equals(s1, s2)
Output
| s1 | s2 | s1_not_equals_s2 |
|---|---|---|
| [1,2,4] | [4,2,1] | [true,false,true] |
Related content
For entire series statistics comparisons, see:
39 - series_outliers()
Scores anomaly points in a series.
The function takes an expression with a dynamic numerical array as input, and generates a dynamic numeric array of the same length. Each value of the array indicates a score of a possible anomaly, using “Tukey’s test”. A value greater than 1.5 in the same element of the input indicates a rise anomaly. A value less than -1.5 indicates a decline anomaly.
Syntax
series_outliers(series [, kind ] [, ignore_val ] [, min_percentile ] [, max_percentile ])
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| series | dynamic | ✔️ | An array of numeric values. |
| kind | string | The algorithm to use for outlier detection. The supported options are "tukey", which is traditional “Tukey”, and "ctukey", which is custom “Tukey”. The default is "ctukey". | |
| ignore_val | int, long, or real | A numeric value indicating the missing values in the series. The default is double(null). The score of nulls and ignore values is set to 0. | |
| min_percentile | int, long, or real | The minimum percentile to use to calculate the normal inter-quantile range. The default is 10. The value must be in the range [2.0, 98.0]. This parameter is only relevant for the "ctukey" kind. | |
| max_percentile | int, long, or real | The maximum percentile to use to calculate the normal inter-quantile range. The default is 90. The value must be in the range [2.0, 98.0]. This parameter is only relevant for the "ctukey" kind. |
The following table describes differences between "tukey" and "ctukey":
| Algorithm | Default quantile range | Supports custom quantile range |
|---|---|---|
"tukey" | 25% / 75% | No |
"ctukey" | 10% / 90% | Yes |
Example
range x from 0 to 364 step 1
| extend t = datetime(2023-01-01) + 1d*x
| extend y = rand() * 10
| extend y = iff(monthofyear(t) != monthofyear(prev(t)), y+20, y) // generate a sample series with outliers at first day of each month
| summarize t = make_list(t), series = make_list(y)
| extend outliers=series_outliers(series)
| extend pos_anomalies = array_iff(series_greater_equals(outliers, 1.5), 1, 0)
| render anomalychart with(xcolumn=t, ycolumns=series, anomalycolumns=pos_anomalies)
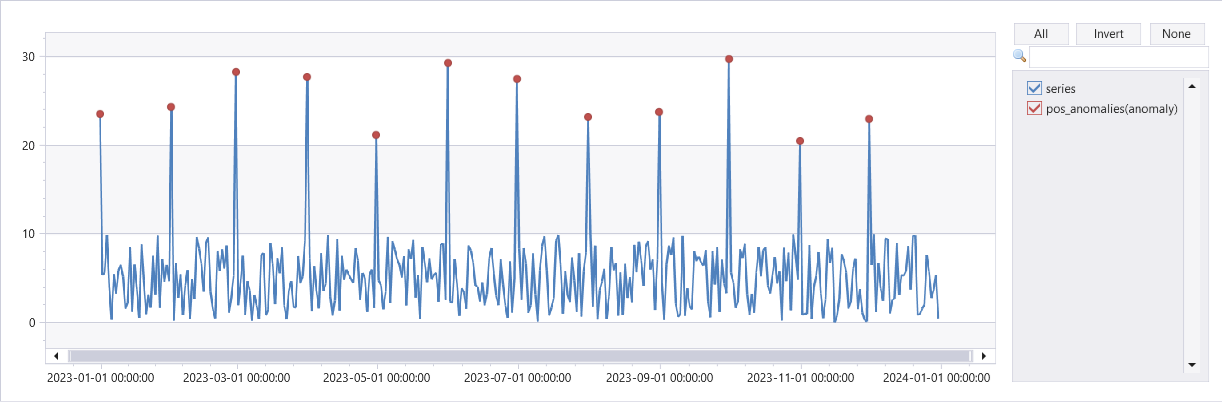
40 - series_pearson_correlation()
Calculates the pearson correlation coefficient of two numeric series inputs.
See: Pearson correlation coefficient.
Syntax
series_pearson_correlation(series1, series2)
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| series1, series2 | dynamic | ✔️ | The arrays of numeric values for calculating the correlation coefficient. |
Returns
The calculated Pearson correlation coefficient between the two inputs. Any non-numeric element or nonexisting element (arrays of different sizes) yields a null result.
Example
range s1 from 1 to 5 step 1
| extend s2 = 2 * s1 // Perfect correlation
| summarize s1 = make_list(s1), s2 = make_list(s2)
| extend correlation_coefficient = series_pearson_correlation(s1, s2)
Output
| s1 | s2 | correlation_coefficient |
|---|---|---|
| [1,2,3,4,5] | [2,4,6,8,10] | 1 |
41 - series_periods_detect()
Finds the most significant periods within a time series.
The series_periods_detect() function is useful for detecting periodic patterns in data, such as daily, weekly, or monthly cycles.
Syntax
series_periods_detect(series, min_period, max_period, num_periods)
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| series | dynamic | ✔️ | An array of numeric values, typically the resulting output of the make-series or make_list operators. |
| min_period | real | ✔️ | The minimal period length for which to search. |
| max_period | real | ✔️ | The maximal period length for which to search. |
| num_periods | long | ✔️ | The maximum number of periods to return. This number is the length of the output dynamic arrays. |
Returns
The function returns a table with two columns:
- periods: A dynamic array containing the periods found, in units of the bin size, ordered by their scores.
- scores: A dynamic array containing values between 0 and 1. Each array measures the significance of a period in its respective position in the periods array.
Example
The following query embeds a snapshot of application traffic for one month. The amount of traffic is aggregated twice a day, meaning the bin size is 12 hours. The query produces a line chart clearly showing a pattern in the data.
print y=dynamic([80, 139, 87, 110, 68, 54, 50, 51, 53, 133, 86, 141, 97, 156, 94, 149, 95, 140, 77, 61, 50, 54, 47, 133, 72, 152, 94, 148, 105, 162, 101, 160, 87, 63, 53, 55, 54, 151, 103, 189, 108, 183, 113, 175, 113, 178, 90, 71, 62, 62, 65, 165, 109, 181, 115, 182, 121, 178, 114, 170])
| project x=range(1, array_length(y), 1), y
| render linechart
You can run the series_periods_detect() function on the same series to identify the recurring patterns. The function searches for patterns in the specified period range and returns two values. The first value indicates a detected pattern that is 14 point long with a score of approximately .84. The other value is zero that indicates no additional pattern was found.
print y=dynamic([80, 139, 87, 110, 68, 54, 50, 51, 53, 133, 86, 141, 97, 156, 94, 149, 95, 140, 77, 61, 50, 54, 47, 133, 72, 152, 94, 148, 105, 162, 101, 160, 87, 63, 53, 55, 54, 151, 103, 189, 108, 183, 113, 175, 113, 178, 90, 71, 62, 62, 65, 165, 109, 181, 115, 182, 121, 178, 114, 170])
| project x=range(1, array_length(y), 1), y
| project series_periods_detect(y, 0.0, 50.0, 2)
Output
| series_periods_detect_y_periods | series_periods_detect_y_periods_scores |
|---|---|
| [14, 0] | [0.84, 0] |
The value in series_periods_detect_y_periods_scores is truncated.
Related content
42 - series_periods_validate()
Checks whether a time series contains periodic patterns of given lengths.
Often a metric measuring the traffic of an application is characterized by a weekly or daily period. This period can be confirmed by running series_periods_validate() that checks for a weekly and daily period.
Syntax
series_periods_validate(series, period1 [ , period2 , . . . ] )
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| series | dynamic | ✔️ | An array of numeric values, typically the resulting output of make-series or make_list operators. |
| period1, period2, etc. | real | ✔️ | The periods to validate in units of the bin size. For example, if the series is in 1h bins, a weekly period is 168 bins. At least one period is required. |
Returns
The function outputs a table with two columns:
- periods: A dynamic array that contains the periods to validate as supplied in the input.
- scores: A dynamic array that contains a score between 0 and 1. The score shows the significance of a period in its respective position in the periods array.
Example
The following query embeds a snapshot of a month of an application’s traffic, aggregated twice a day (the bin size is 12 hours).
print y=dynamic([80, 139, 87, 110, 68, 54, 50, 51, 53, 133, 86, 141, 97, 156, 94, 149, 95, 140, 77, 61, 50, 54, 47, 133, 72, 152, 94, 148, 105, 162, 101, 160, 87, 63, 53, 55, 54, 151, 103, 189, 108, 183, 113, 175, 113, 178, 90, 71, 62, 62, 65, 165, 109, 181, 115, 182, 121, 178, 114, 170])
| project x=range(1, array_length(y), 1), y
| render linechart

If you run series_periods_validate() on this series to validate a weekly period (14 points long) it results in a high score, and with a 0 score when you validate a five-day period (10 points long).
print y=dynamic([80, 139, 87, 110, 68, 54, 50, 51, 53, 133, 86, 141, 97, 156, 94, 149, 95, 140, 77, 61, 50, 54, 47, 133, 72, 152, 94, 148, 105, 162, 101, 160, 87, 63, 53, 55, 54, 151, 103, 189, 108, 183, 113, 175, 113, 178, 90, 71, 62, 62, 65, 165, 109, 181, 115, 182, 121, 178, 114, 170])
| project x=range(1, array_length(y), 1), y
| project series_periods_validate(y, 14.0, 10.0)
Output
| series_periods_validate_y_periods | series_periods_validate_y_scores |
|---|---|
| [14.0, 10.0] | [0.84, 0.0] |
43 - series_seasonal()
Calculates the seasonal component of a series, according to the detected or given seasonal period.
Syntax
series_seasonal(series [, period ])
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| series | dynamic | ✔️ | An array of numeric values. |
| period | int | The number of bins for each seasonal period. This value can be any positive integer. By default, the value is set to -1, which automatically detects the period using the series_periods_detect() with a threshold of 0.7. If seasonality is not detected, the function returns zeros. If a different value is set, it ignores seasonality and returns a series of zeros. |
Returns
A dynamic array of the same length as the series input that contains the calculated seasonal component of the series. The seasonal component is calculated as the median of all the values that correspond to the location of the bin, across the periods.
Examples
Auto detect the period
In the following example, the series’ period is automatically detected. The first series’ period is detected to be six bins and the second five bins. The third series’ period is too short to be detected and returns a series of zeroes. See the next example on how to force the period.
print s=dynamic([2, 5, 3, 4, 3, 2, 1, 2, 3, 4, 3, 2, 1, 2, 3, 4, 3, 2, 1, 2, 3, 4, 3, 2, 1])
| union (print s=dynamic([8, 12, 14, 12, 10, 10, 12, 14, 12, 10, 10, 12, 14, 12, 10, 10, 12, 14, 12, 10]))
| union (print s=dynamic([1, 3, 5, 2, 4, 6, 1, 3, 5, 2, 4, 6]))
| extend s_seasonal = series_seasonal(s)
Output
| s | s_seasonal |
|---|---|
| [2,5,3,4,3,2,1,2,3,4,3,2,1,2,3,4,3,2,1,2,3,4,3,2,1] | [1.0,2.0,3.0,4.0,3.0,2.0,1.0,2.0,3.0,4.0,3.0,2.0,1.0,2.0,3.0,4.0,3.0,2.0,1.0,2.0,3.0,4.0,3.0,2.0,1.0] |
| [8,12,14,12,10,10,12,14,12,10,10,12,14,12,10,10,12,14,12,10] | [10.0,12.0,14.0,12.0,10.0,10.0,12.0,14.0,12.0,10.0,10.0,12.0,14.0,12.0,10.0,10.0,12.0,14.0,12.0,10.0] |
| [1,3,5,2,4,6,1,3,5,2,4,6] | [0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0] |
Force a period
In this example, the series’ period is too short to be detected by series_periods_detect(), so we explicitly force the period to get the seasonal pattern.
print s=dynamic([1, 3, 5, 1, 3, 5, 2, 4, 6])
| union (print s=dynamic([1, 3, 5, 2, 4, 6, 1, 3, 5, 2, 4, 6]))
| extend s_seasonal = series_seasonal(s, 3)
Output
| s | s_seasonal |
|---|---|
| [1,3,5,1,3,5,2,4,6] | [1.0,3.0,5.0,1.0,3.0,5.0,1.0,3.0,5.0] |
| [1,3,5,2,4,6,1,3,5,2,4,6] | [1.5,3.5,5.5,1.5,3.5,5.5,1.5,3.5,5.5,1.5,3.5,5.5] |
Related content
44 - series_sign()
Calculates the element-wise sign of the numeric series input.
Syntax
series_sign(series)
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| series | dynamic | ✔️ | An array of numeric values over which the sign function is applied. |
Returns
A dynamic array of calculated sign function values. -1 for negative, 0 for 0, and 1 for positive. Any non-numeric element yields a null element value.
Example
print arr = dynamic([-6, 0, 8])
| extend arr_sign = series_sign(arr)
Output
| arr | arr_sign |
|---|---|
| [-6,0,8] | [-1,0,1] |
45 - series_sin()
Calculates the element-wise sine of the numeric series input.
Syntax
series_sin(series)
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| series | dynamic | ✔️ | An array of numeric values over which the sine function is applied. |
Returns
A dynamic array of calculated sine function values. Any non-numeric element yields a null element value.
Example
print arr = dynamic([-1, 0, 1])
| extend arr_sin = series_sin(arr)
Output
| arr | arr_sin |
|---|---|
| [-6.5,0,8.2] | [-0.8414709848078965,0.0,0.8414709848078965] |
46 - series_stats_dynamic()
Returns statistics for a series in a dynamic object.
Syntax
series_stats_dynamic(series [, ignore_nonfinite ])
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| series | dynamic | ✔️ | An array of numeric values. |
| ignore_nonfinite | bool | Indicates whether to calculate the statistics while ignoring non-finite values, such as null, NaN, inf, and so on. The default is false, which returns null if non-finite values are present in the array. |
Returns
A dynamic property bag object with the following content:
min: The minimum value in the input array.min_idx: The first position of the minimum value in the input array.max: The maximum value in the input array.max_idx: The first position of the maximum value in the input array.avg: The average value of the input array.variance: The sample variance of input array.stdev: The sample standard deviation of the input array.sum: The sum of the values in the input array.len: The length of the input array.
Example
print x=dynamic([23, 46, 23, 87, 4, 8, 3, 75, 2, 56, 13, 75, 32, 16, 29])
| project stats=series_stats_dynamic(x)
Output
| stats |
|---|
| {“min”: 2.0, “min_idx”: 8, “max”: 87.0, “max_idx”: 3, “avg”: 32.8, “stdev”: 28.503633853548269, “variance”: 812.45714285714291, “sum”: 492.0, “len”: 15} |
The following query creates a series of the average taxi fare per minute, and then calculates statistics on these average fares:
nyc_taxi
| make-series Series=avg(fare_amount) on pickup_datetime step 1min
| project Stats=series_stats_dynamic(Series)
Output
| Stats |
|---|
| {“min”:0,“min_idx”:96600,“max”:“31.779069767441861”,“max_idx”:481260,“avg”:“13.062685479531414”,“stdev”:“1.7730590207741219”,“variance”:“3.1437382911484884”,“sum”:“6865747.488041711”,“len”:525600} |
47 - series_stats()
Returns statistics for a numerical series in a table with a column for each statistic.
Syntax
... | extend ( Name, … ) = series_stats ( series [, ignore_nonfinite] )
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| Name | string | The column labels for the output table. If not provided, the system will generate them. If you provide a limited number of names, the table will show only those columns. | |
| series | dynamic | ✔️ | An array of numeric values. |
| ignore_nonfinite | bool | Determines if the calculation includes non-finite values like null, NaN, inf, and so on. The default is false, which will result in null if non-finite values are present. |
Returns
A table with a column for each of the statistics displayed in the following table.
| Statistic | Description |
|---|---|
min | The minimum value in the input array. |
min_idx | The first position of the minimum value in the input array. |
max | The maximum value in the input array. |
max_idx | The first position of the maximum value in the input array. |
avg | The average value of the input array. |
variance | The sample variance of input array. |
stdev | The sample standard deviation of the input array. |
Example
print x=dynamic([23, 46, 23, 87, 4, 8, 3, 75, 2, 56, 13, 75, 32, 16, 29])
| project series_stats(x)
Output
| series_stats_x_min | series_stats_x_min_idx | series_stats_x_max | series_stats_x_max_idx | series_stats_x_avg | series_stats_x_stdev | series_stats_x_variance |
|---|---|---|---|---|---|---|
| 2 | 8 | 87 | 3 | 32.8 | 28.5036338535483 | 812.457142857143 |
48 - series_subtract()
Calculates the element-wise subtraction of two numeric series inputs.
Syntax
series_subtract(series1, series2)
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| series1, series2 | dynamic | ✔️ | Arrays of numeric values, the second array to be element-wise subtracted from the first array. |
Returns
A dynamic array of calculated element-wise subtract operation between the two inputs. Any non-numeric element or non-existing element, such as in the case of arrays of different sizes, yields a null element value.
Example
range x from 1 to 3 step 1
| extend y = x * 2
| extend z = y * 2
| project s1 = pack_array(x,y,z), s2 = pack_array(z, y, x)
| extend s1_subtract_s2 = series_subtract(s1, s2)
Output
| s1 | s2 | s1_subtract_s2 |
|---|---|---|
| [1,2,4] | [4,2,1] | [-3,0,3] |
| [2,4,8] | [8,4,2] | [-6,0,6] |
| [3,6,12] | [12,6,3] | [-9,0,9] |
49 - series_sum()
Calculates the sum of series elements.
Syntax
series_sum(series)
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| series | dynamic | ✔️ | Array of numeric values. |
Returns
Returns a double type value with the sum of the elements of the array.
Example
print arr=dynamic([1,2,3,4])
| extend series_sum=series_sum(arr)
Output
| s1 | series_sum |
|---|---|
| [1,2,3,4] | 10 |
50 - series_tan()
Calculates the element-wise tangent of the numeric series input.
Syntax
series_tan(series)
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| series | dynamic | ✔️ | An array of numeric values on which the tangent function is applied. |
Returns
A dynamic array of calculated tangent function values. Any non-numeric element yields a null element value.
Example
print arr = dynamic([-1, 0, 1])
| extend arr_tan = series_tan(arr)
Output
| arr | arr_tan |
|---|---|
| [-6.5,0,8.2] | [-1.5574077246549023,0.0,1.5574077246549023] |
51 - series_asin()
Calculates the element-wise arcsine function of the numeric series input.
Syntax
series_asin(series)
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| series | dynamic | ✔️ | An array of numeric values over which the arcsine function is applied. |
Returns
Dynamic array of calculated arcsine function values. Any non-numeric element yields a null element value.
Example
The following example creates a dynamic array, arr, with the value [-1,0,1]. It then extends the results with column arr_asin, containing the results of the series_asin() function applied to the arr array.
print arr = dynamic([-1,0,1])
| extend arr_asin = series_asin(arr)
Output
| arr | arr_asin |
|---|---|
| [-1,0,1] | ["-1.5707963267948966",0,“1.5707963267948966”] |
52 - series_ceiling()
Calculates the element-wise ceiling function of the numeric series input.
Syntax
series_ceiling(series)
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| series | dynamic | ✔️ | An array of numeric values over which the ceiling function is applied. |
Returns
Dynamic array of the calculated ceiling function. Any non-numeric element yields a null element value.
Example
print s = dynamic([-1.5,1,2.5])
| extend s_ceiling = series_ceiling(s)
Output
| s | s_ceiling |
|---|---|
| [-1.5,1,2.5] | [-1.0,1.0,3.0] |
53 - series_pow()
Calculates the element-wise power of two numeric series inputs.
Syntax
series_pow(series1, series2)
Parameters
| Name | Type | Required | Description |
|---|---|---|---|
| series1, series2 | dynamic | ✔️ | Arrays of numeric values. The first array, or base, is element-wise raised to the power of the second array, or power, into a dynamic array result. |
Returns
A dynamic array of calculated element-wise power operation between the two inputs. Any non-numeric element or non-existing element, such as in the case of arrays of different sizes, yields a null element value.
Example
print x = dynamic([1, 2, 3, 4]), y=dynamic([1, 2, 3, 0.5])
| extend x_pow_y = series_pow(x, y)
Output
| x | y | x_pow_y |
|---|---|---|
| [1,2,3,4] | [1,2,3,0.5] | [1.0,4.0,27.0,2.0] |